Использование машинного обучения для анализа временных рядов
прогнозирование временных рядов с помощью одновременного использования нескольких моделей в языке программирования R
Под временным рядом обычно понимается последовательность {\(y_t\)}, элементы которой принимают значения через определенные (обычно регулярные) значения времени \(t\). Область применения временных рядов очень обширна, временные ряды используются в сейсмологии, метеорологии, экономике, при регистрации значений любых датчиков. Временным рядам посвящено большое количество литературы, в частности, работа с временными рядами в среде R описана в монографиях [Shumway & Stoffer], [Hyndman & Athanasopoulos] и [Мастицкий].
В нашем случае, в качестве временных рядов рассматривается, например, количество пожаров, регистрируемых в сутки/неделю/месяц или уровень воды в реках. Мы покажем применение достаточно новой библиотеки modeltime для моделирования временных рядов с помощью методов машинного обучения. Основные преимущества данной библиотеки:
- использование современных алогритмов машинного обучения;
- комбинирование нескольких алгоритмов для улучшения результата;
- работа с несколькими моделями одновременно;
- настройка гиперпараметров моделей.
Библиотека modeltime интегрирована с библиотекой tidymodels, что позволяет рассматривать ее в рамках единой экосистемы алгоритмов машинного обучения, основанной на принципах tidy data. Узнать больше о библиотеке tidymodels можно на сайте библиотеки и из новой книги [Kuhn & Silge].
Установка библиотеки
Стабильную версию библиотеки можно установить из репозитория CRAN соответствующей командой:
install.packages("modeltime")Девелоперская версия доступна на GitHub:
remotes::install_github("business-science/modeltime")Исходные данные
Подключим небходимые библиотеки.
library(readxl)
library(magrittr)
library(tidyverse)
library(lubridate)
library(tidymodels)
library(modeltime)
library(timetk)Рассмотрим фондовые данные по гидрологии в Российской Федерации 🇷🇺 за 2008-2015 года1. Загрузим данные с GitHub:
url <- "https://raw.githubusercontent.com/materov/blog_data/main/df_hydro.csv"
df_hydro <- readr::read_csv(url)Исходные данные содержат 615 849 записей и имеют две переменных: date и level, отвечающих за дату наблюдения и уровень воды в метрах над нулем графика поста.
df_hydro## # A tibble: 615,849 x 2
## date level
## <dttm> <dbl>
## 1 2013-10-11 00:00:00 626
## 2 2013-11-11 00:00:00 642
## 3 2013-12-11 00:00:00 615
## 4 2013-01-12 00:00:00 549
## 5 2013-02-12 00:00:00 543
## 6 2013-03-12 00:00:00 542
## 7 2013-04-12 00:00:00 541
## 8 2013-05-12 00:00:00 705
## 9 2013-06-12 00:00:00 916
## 10 2013-07-12 00:00:00 653
## # … with 615,839 more rowsСформируем данные для временного ряда: рассмотрим максимальные значения уровня воды.
fire_time_series_tbl <-
df_hydro %>%
group_by(date) %>%
summarise(value = max(level)) Преобразуем date в формат даты:
fire_time_series_tbl$date %<>% as.Date()Визуализируем получившийся временной ряд:
fire_time_series_tbl %>%
ggplot(aes(x = date, y = value)) + geom_line()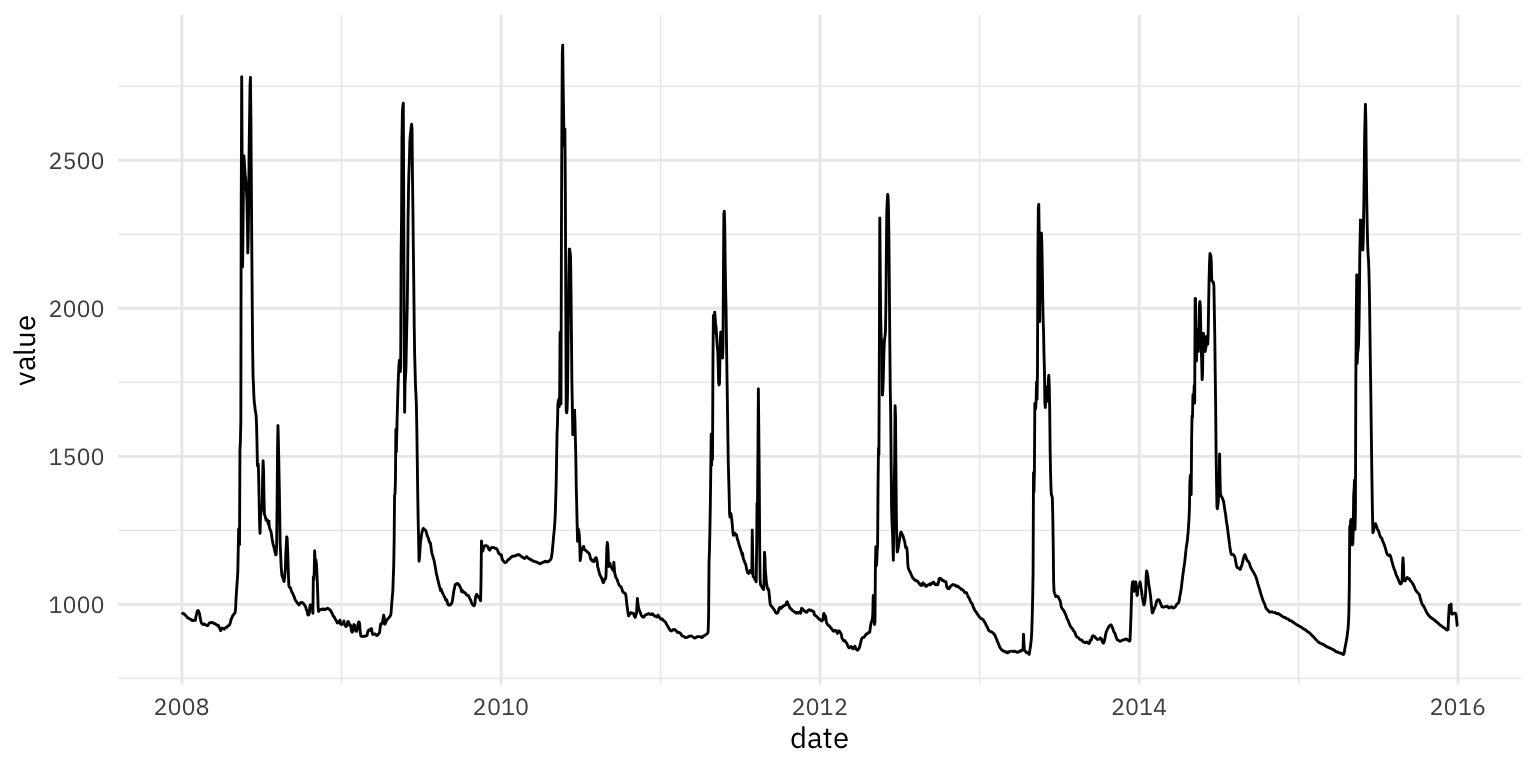
Рисунок 1: Исходный временной ряд
Из графика видно, что временной ряд имеет периодический характер.
Моделирование временных рядов
Весь поток операций в modeltime можно разбить на следующие 6 шагов, позволяющих выполнить:
- Сбор данных и разделение их на обучающую и тестовую выборки.
- Создание и подгонку нескольких моделей.
- Добавление подогнанных моделей в таблицы моделей.
- Калибровка моделей на тестовое множество.
- Выполнение прогноза для тестового множества и оценка точности.
- Корректировку моделей на полный набор данных и прогнозирование на будущие значения.
Кратко покажем реализацию этих шагов. Ниже показана иллюстрация оптимизированного рабочего процесса, рассмотренная на сайте библиотеки.

Иллюстрация оптимизированного рабочего процесса прогнозирования временного ряда
Шаг 1. Разбиение на обучающую и тестовую выборку можно делать либо указав временной параметр, либо процентные соотношения.
# Разделение выборки на обучающую и тестовую ---------------------------------
# разбиение в соотношении 90% / 10%
splits <- fire_time_series_tbl %>%
rsample::initial_time_split(prop = 0.9)
# альтернативный вариант
# splits <- fire_time_series_tbl %>%
# time_series_split(assess = "2 months",
# cumulative = TRUE)splits %>%
tk_time_series_cv_plan() %>%
plot_time_series_cv_plan(date, value,
.interactive = FALSE) +
labs(title = "Разделение временного ряда на обучающую и тестовую выборку",
subtitle = "в качестве тестовой выборки рассмотрены 10% данных",
color = "Выборка:") +
scale_x_date(date_breaks = "12 months",
date_labels = "%Y")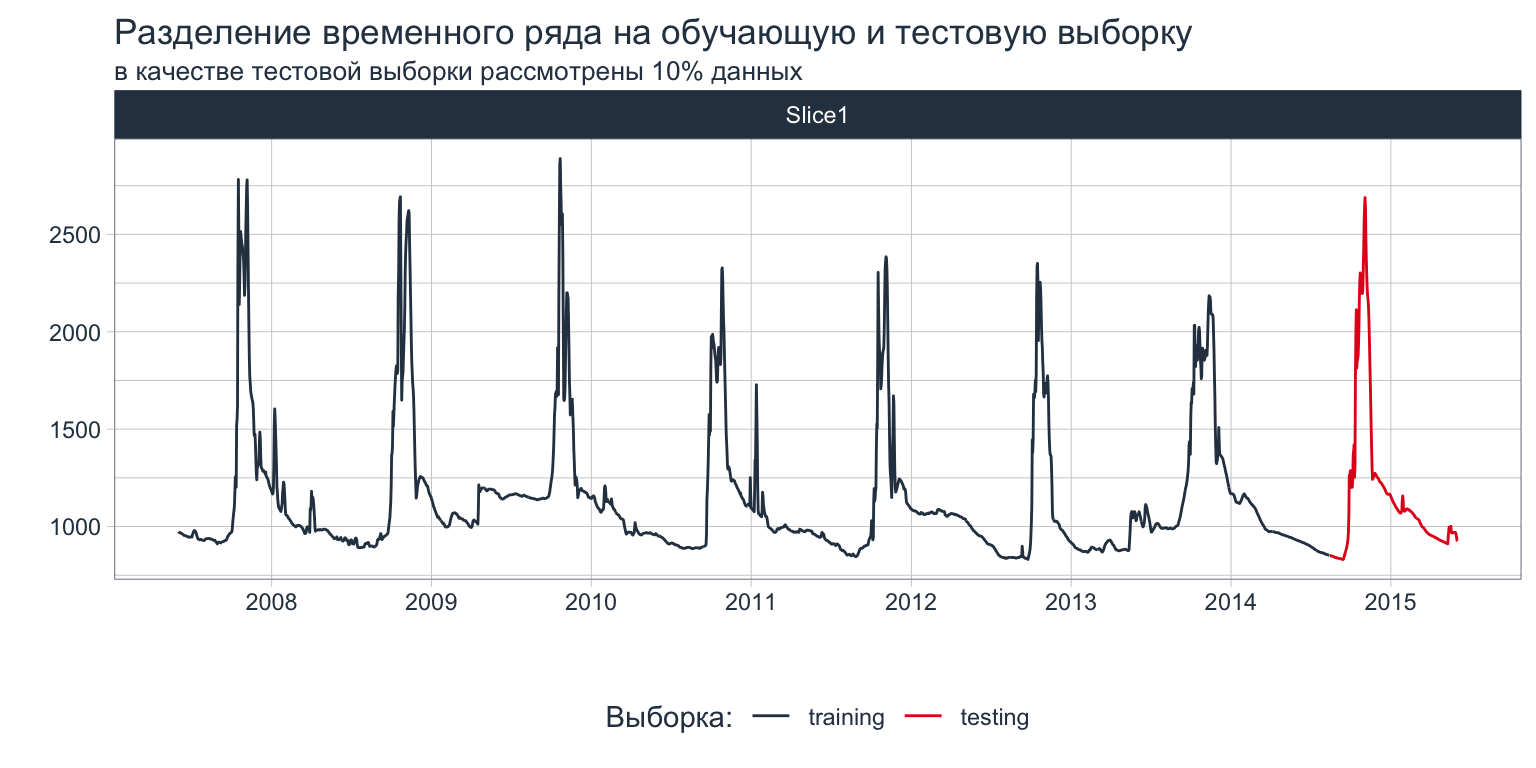
Рисунок 2: Пример разделения временного ряда на обучающую и тестовую выборку
Шаг 2. Следующим этапом является создание и подгонка моделей. Ключевая особенность modeltime заключается в возможности работы с несколькими моделями одновременно. Это позволяет сравнивать модели, выбирая наилучшие результаты.
Вот некоторые стандартные модели встроенные в modeltime (полный список моделей, который постоянно дополняется, можно получить на сайте библиотеки):
- ARIMA;
- линейная регрессия;
- экспоненциальное сглаживание;
- Prophet;
- MARS (Multivariate Adaptive Regression Splines);
- Elastic Nets;
- Random Forest.
Отметим, что modeltime позволяет комбинировать алгоритмы, улучшая их, например, в модели Prophet можно улучшить ошибки, используя известный алгоритм машинного обучения XGBoost, что дает новую модель, которая называется Prophet Boost.
Модели машинного обучения более сложны, чем автоматизированные модели. Эта сложность обычно требует рабочего процесса (иногда называемого конвейером в других языках программирования). Общий процесс протекает следующим образом:
- Создание типа модели, так называемого рецепта (recipe) предварительной обработки используя
tidymodels. - Создание спецификаций модели.
- Использование рабочего процесса для объединения спецификаций модели, предобработки и подходящей модели.
Построим несколько моделей для данного временного ряда.
- Линейная регрессия
# Создание и подгонка нескольких моделей -------------------------------------
# Модель 1: lm ----
# Линейная регрессия
model_fit_lm <- linear_reg() %>%
set_engine("lm") %>%
fit(value ~ as.numeric(date) + factor(month(date), ordered = FALSE),
data = training(splits))- Классическая модель ARIMA с автоопределением параметров
# Модель 2: auto_arima ----
# ARIMA
model_fit_arima <- arima_reg() %>%
set_engine(engine = "auto_arima") %>%
fit(value ~ date, data = training(splits))- Модель ARIMA Boost
# Модель 3: arima_boost ----
# ARIMA с бустингом (уменьшение ошибок с помощью XGBoost)
model_fit_arima_boosted <- arima_boost(
min_n = 2,
learn_rate = 0.015) %>%
set_engine(engine = "auto_arima_xgboost") %>%
fit(value ~ date + as.numeric(date) +
factor(month(date), ordered = F),
data = training(splits))- Модель ETS
# Модель 4: ets ----
# экспоненциальное сглаживание
model_fit_ets <- exp_smoothing() %>%
set_engine(engine = "ets") %>%
fit(value ~ date, data = training(splits))- Модель Prophet
# Модель 5: prophet ----
# Prophet от Facebook
model_fit_prophet <- prophet_reg() %>%
set_engine("prophet",
yearly.seasonality = TRUE) %>%
fit(value ~ date, training(splits))- Модель MARS
# Модель 6: MARS ----
# Пример "рецепта" предобработки
recipe_spec <- recipe(value ~ date, data = training(splits)) %>%
step_date(date, features = "month", ordinal = FALSE) %>%
step_mutate(date_num = as.numeric(date)) %>%
step_normalize(date_num) %>%
step_rm(date)# вид "рецепта"
recipe_spec %>% prep() %>% juice()## # A tibble: 2,629 x 3
## value date_month date_num
## <dbl> <fct> <dbl>
## 1 973 янв -1.73
## 2 971 янв -1.73
## 3 969 янв -1.73
## 4 968 янв -1.73
## 5 969 янв -1.73
## 6 968 янв -1.72
## 7 966 янв -1.72
## 8 965 янв -1.72
## 9 963 янв -1.72
## 10 962 янв -1.72
## # … with 2,619 more rows# спецификации модели MARS (Computational engine: earth)
model_spec_mars <- mars(mode = "regression") %>%
set_engine("earth")# собираем модель MARS
workflow_fit_mars <- workflow() %>%
add_recipe(recipe_spec) %>%
add_model(model_spec_mars) %>%
fit(training(splits))- Модель Prophet Boost
# Модель 7: Prophet Boost ----
# рецепт
recipe_spec <- recipe(value ~ date, training(splits)) %>%
step_timeseries_signature(date) %>%
step_rm(contains("am.pm"), contains("hour"), contains("minute"),
contains("second"), contains("xts")) %>%
step_fourier(date, period = 365, K = 5) %>%
step_dummy(all_nominal())# спецификации
model_spec_prophet_boost <- prophet_boost() %>%
set_engine("prophet_xgboost", yearly.seasonality = TRUE)# сборка модели
workflow_fit_prophet_boost <- workflow() %>%
add_model(model_spec_prophet_boost) %>%
add_recipe(recipe_spec) %>%
fit(training(splits))- Модель glmnet
# Модель 8: glmnet ----
# recipe
recipe_spec <- recipe(value ~ date, training(splits)) %>%
step_timeseries_signature(date) %>%
step_rm(contains("am.pm"), contains("hour"), contains("minute"),
contains("second"), contains("xts")) %>%
step_fourier(date, period = 365, K = 5) %>%
step_dummy(all_nominal())# просмотр "рецепта"
recipe_spec %>% prep() %>% juice()## # A tibble: 2,629 x 47
## date value date_index.num date_year date_year.iso date_half
## <date> <dbl> <dbl> <int> <int> <int>
## 1 2008-01-01 973 1199145600 2008 2008 1
## 2 2008-01-02 971 1199232000 2008 2008 1
## 3 2008-01-03 969 1199318400 2008 2008 1
## 4 2008-01-04 968 1199404800 2008 2008 1
## 5 2008-01-05 969 1199491200 2008 2008 1
## 6 2008-01-06 968 1199577600 2008 2008 1
## 7 2008-01-07 966 1199664000 2008 2008 1
## 8 2008-01-08 965 1199750400 2008 2008 1
## 9 2008-01-09 963 1199836800 2008 2008 1
## 10 2008-01-10 962 1199923200 2008 2008 1
## # … with 2,619 more rows, and 41 more variables: date_quarter <int>,
## # date_month <int>, date_day <int>, date_wday <int>, date_mday <int>,
## # date_qday <int>, date_yday <int>, date_mweek <int>, date_week <int>,
## # date_week.iso <int>, date_week2 <int>, date_week3 <int>, date_week4 <int>,
## # date_mday7 <int>, date_sin365_K1 <dbl>, date_cos365_K1 <dbl>,
## # date_sin365_K2 <dbl>, date_cos365_K2 <dbl>, date_sin365_K3 <dbl>,
## # date_cos365_K3 <dbl>, date_sin365_K4 <dbl>, date_cos365_K4 <dbl>,
## # date_sin365_K5 <dbl>, date_cos365_K5 <dbl>, date_month.lbl_01 <dbl>,
## # date_month.lbl_02 <dbl>, date_month.lbl_03 <dbl>, date_month.lbl_04 <dbl>,
## # date_month.lbl_05 <dbl>, date_month.lbl_06 <dbl>, date_month.lbl_07 <dbl>,
## # date_month.lbl_08 <dbl>, date_month.lbl_09 <dbl>, date_month.lbl_10 <dbl>,
## # date_month.lbl_11 <dbl>, date_wday.lbl_1 <dbl>, date_wday.lbl_2 <dbl>,
## # date_wday.lbl_3 <dbl>, date_wday.lbl_4 <dbl>, date_wday.lbl_5 <dbl>,
## # date_wday.lbl_6 <dbl># спецификация модели
model_spec_glmnet <- linear_reg(penalty = 0.01, mixture = 0.5) %>%
set_engine("glmnet")# сборка модели glmnet
workflow_fit_glmnet <- workflow() %>%
add_model(model_spec_glmnet) %>%
add_recipe(recipe_spec %>% step_rm(date)) %>%
fit(training(splits))- Модель Random Forest
# Модель 9: Random Forest ----
model_spec_rf <- rand_forest(trees = 500, min_n = 50) %>%
set_engine("randomForest")# сборка модели Random Forest
workflow_fit_rf <- workflow() %>%
add_model(model_spec_rf) %>%
add_recipe(recipe_spec %>% step_rm(date)) %>%
fit(training(splits))Шаг 3. Модели прописываются и добавляются в единую таблицу моделей, в которой до включения можно настраивать параметры, а затем проходит их подгонка/масштабирование, проверка на соответствие и калибровка по отношению к тестовой выборке. Далее происходит оценка качества моделей на тестовой выборке используя различные показатели точности:
- MAE – средняя абсолютная ошибка;
- MAPE – средняя абсолютная процентная ошибка;
- MASE – средняя абсолютная нормированная ошибка;
- SMAPE – симметричная средняя абсолютная процентная ошибка;
- RMSE – среднеквадратическая ошибка;
- RSQ – показатель \(R^2\).
# Добавление подогнанных моделей в таблицы моделей ------------------------
models_tbl <- modeltime_table(
model_fit_lm,
model_fit_arima,
model_fit_arima_boosted,
model_fit_ets,
model_fit_prophet,
# модели машинного обучения
workflow_fit_mars,
workflow_fit_prophet_boost,
workflow_fit_glmnet,
workflow_fit_rf
)# просмотр таблицы моделей
models_tbl## # Modeltime Table
## # A tibble: 9 x 3
## .model_id .model .model_desc
## <int> <list> <chr>
## 1 1 <fit[+]> LM
## 2 2 <fit[+]> ARIMA(5,0,4) WITH NON-ZERO MEAN
## 3 3 <fit[+]> ARIMA(4,0,5) WITH NON-ZERO MEAN W/ XGBOOST ERRORS
## 4 4 <fit[+]> ETS(M,AD,N)
## 5 5 <fit[+]> PROPHET
## 6 6 <workflow> EARTH
## 7 7 <workflow> PROPHET W/ XGBOOST ERRORS
## 8 8 <workflow> GLMNET
## 9 9 <workflow> RANDOMFORESTШаг 4. Калибровка, по сути, – это способ определения доверительных интервалов и метрик точности, при этом калибровочные данные – это спрогнозированные значения и невязки, которые вычисляются на основе данных вне выборки.
# Калибровка --------------------------------------------------------------
calibration_tbl <- models_tbl %>%
modeltime_calibrate(new_data = testing(splits))# таблица калиброванных моделей
# добавились .type и .calibration_data
calibration_tbl## # Modeltime Table
## # A tibble: 9 x 5
## .model_id .model .model_desc .type .calibration_data
## <int> <list> <chr> <chr> <list>
## 1 1 <fit[+]> LM Test <tibble [293 × 4…
## 2 2 <fit[+]> ARIMA(5,0,4) WITH NON-ZERO MEAN Test <tibble [293 × 4…
## 3 3 <fit[+]> ARIMA(4,0,5) WITH NON-ZERO MEAN W… Test <tibble [293 × 4…
## 4 4 <fit[+]> ETS(M,AD,N) Test <tibble [293 × 4…
## 5 5 <fit[+]> PROPHET Test <tibble [293 × 4…
## 6 6 <workflo… EARTH Test <tibble [293 × 4…
## 7 7 <workflo… PROPHET W/ XGBOOST ERRORS Test <tibble [293 × 4…
## 8 8 <workflo… GLMNET Test <tibble [293 × 4…
## 9 9 <workflo… RANDOMFOREST Test <tibble [293 × 4…Шаг 5. Сформированные модели проверяются на тестовых данных и визуализируются.
calibration_tbl %>%
modeltime_forecast(new_data = testing(splits),
actual_data = fire_time_series_tbl) %>%
filter(.index > "2012-01-01") %>%
plot_modeltime_forecast(.interactive = F) +
labs(color = "Модели:",
title = "Прогнозирование временного ряда на тестовую выборку") +
guides(color = guide_legend(ncol = 3))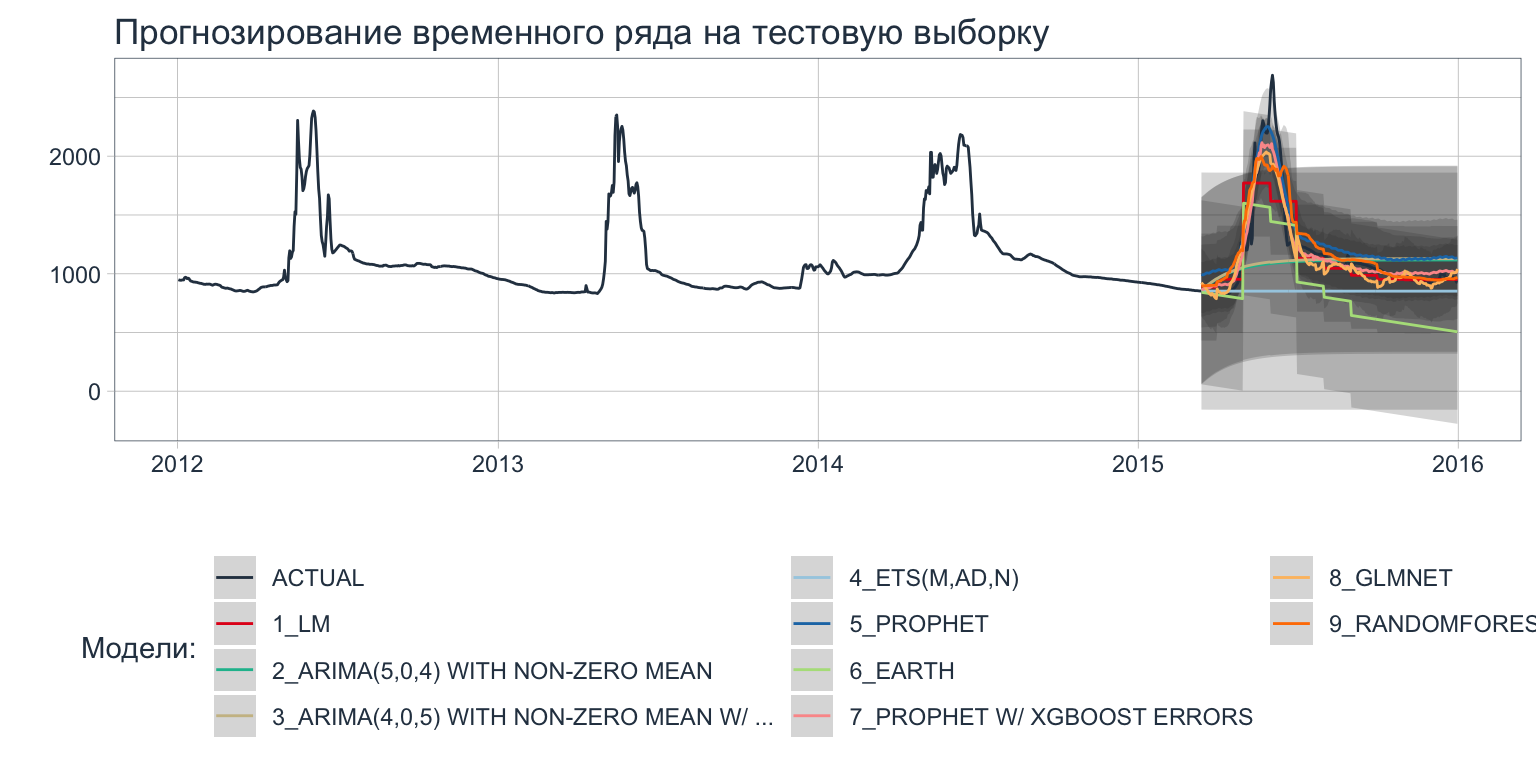
Рисунок 3: Пример прогнозирования временного ряда на тестовую выборку
Также, составляется таблица ошибок, использующая рассмотренные выше показатели точности, пример такого рода таблицы показан ниже.
# таблица ошибок
calibration_tbl %>%
modeltime_accuracy() %>%
table_modeltime_accuracy(.interactive = F) | .model_id | .model_desc | .type | mae | mape | mase | smape | rmse | rsq |
|---|---|---|---|---|---|---|---|---|
| 1 | LM | Test | 134.13 | 9.46 | 7.12 | 9.50 | 232.13 | 0.68 |
| 2 | ARIMA(5,0,4) WITH NON-ZERO MEAN | Test | 233.95 | 16.09 | 12.42 | 17.72 | 406.55 | 0.02 |
| 3 | ARIMA(4,0,5) WITH NON-ZERO MEAN W/ XGBOOST ERRORS | Test | 235.84 | 16.42 | 12.52 | 17.91 | 403.69 | 0.02 |
| 4 | ETS(M,AD,N) | Test | 325.55 | 22.08 | 17.28 | 27.24 | 514.37 | 0.02 |
| 5 | PROPHET | Test | 148.64 | 13.76 | 7.89 | 12.76 | 166.18 | 0.94 |
| 6 | EARTH | Test | 344.41 | 29.04 | 18.29 | 35.21 | 399.23 | 0.61 |
| 7 | PROPHET W/ XGBOOST ERRORS | Test | 74.83 | 5.79 | 3.97 | 5.75 | 117.65 | 0.94 |
| 8 | GLMNET | Test | 92.95 | 6.89 | 4.94 | 7.02 | 148.54 | 0.89 |
| 9 | RANDOMFOREST | Test | 108.05 | 8.14 | 5.74 | 7.77 | 180.18 | 0.81 |
Шаг 6. Заключительный этап состоит в том, чтобы скорректировать модели, распространить их на полный набор данных и спрогнозировать будущие значения.
refit_tbl <- calibration_tbl %>%
filter(.model_id != 1) %>%
filter(.model_id != 2) %>%
filter(.model_id != 3) %>%
filter(.model_id != 4) %>%
filter(.model_id != 6) %>%
modeltime_refit(data = fire_time_series_tbl)Визуализируем прогноз на 1 год вперед.
refit_tbl %>%
modeltime_forecast(h = "1 year", actual_data = fire_time_series_tbl) %>%
filter(.index > "2014-01-01") %>%
plot_modeltime_forecast(.interactive = FALSE) +
labs(title = "Скорректированный прогноз для различных моделей",
subtitle = "прогноз на 1 год вперед",
color = "Модели:") +
scale_x_date(date_breaks = "1 year",
date_labels = "%Y") 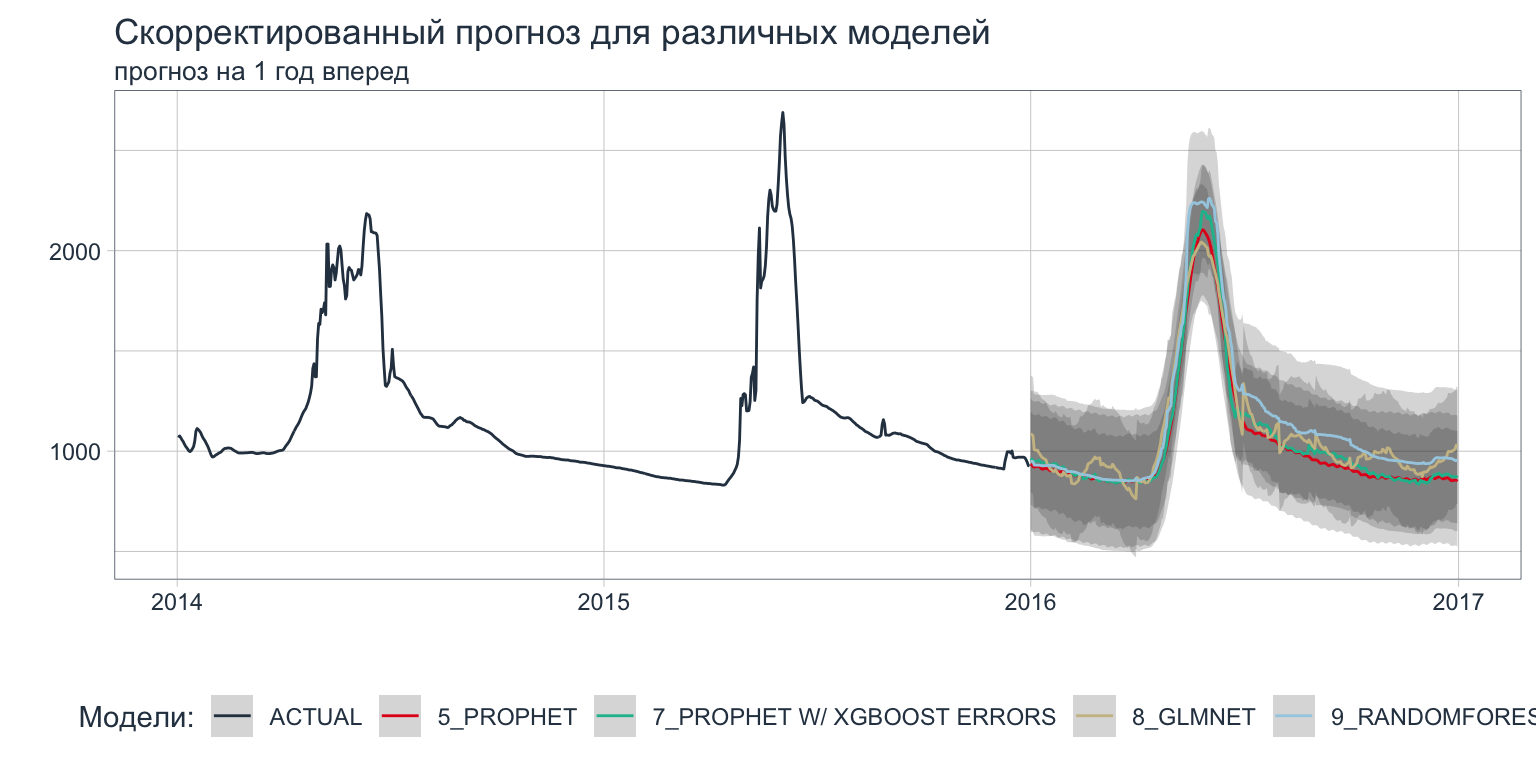
Рисунок 4: Прогноз временного ряда с использованием нескольких моделей
Заключение
Мы рассмотрели методы прогнозирования временных рядов на основе современных алгоритмов машинного обучения для составления гидрологического прогноза, что публикуется впервые в применении в вопросам природной и техносферной безопасности. Используя возможности языка программирования R можно не только разрабатывать модели прогнозирования, но и в последующем делать на их основе актуальные аналитические веб-сервисы на основе R Markdown и Shiny для практического применения прогнозов, что представляется перспективным направлением.
Отметим, что для улучшения точности прогноза сильно неструктурированных данных, например, при отсутствии явно выраженных сезонных компонент, можно использовать для моделирования нейронные (как правило, RNN, LSTM или CNN) сети, однако это выходит за рамки настоящей статьи, и обучение нейронной сети, – процесс гораздо более трудоемкий, чем рассмотренное в работе моделирование, что может оказаться неэффективным с точки зрения временных затрат.
Автор выражает благодарность В.В. Ничепорчуку за предоставленные данные.↩︎