Анализ графа дорожной сети
пример анализа графа дорожной сети города с использованием библиотеки sfnetworks
Базовая карта на основе сервиса OpenStreetMap
Для анализа топологии дорожной сети города существует множество различных инструментов. Например, библиотека Network analysis library геоинформационной системы QGIS позволяет на основе географических данных (линейных векторных слоев) создавать графы как структуры данных и работать с ними как с математическими объектами, а также использовать дополнения, написанные на языке Python.
В языке программирования R существует библиотека sfnetworks, цель которой – работа с геопространственными сетями, т.е. графами, встроенными в географическое пространство. Это означает, что как узлы, так и ребра графа могут быть представлены в виде географических объектов. Такие структуры играют важную роль во многих различных областях, начиная от транспортного планирования и логистики, заканчивая экологией и эпидемиологией.
Библиотека sfnetworks сочетает возможности двух популярных библиотек: sf, учитывающей пространственные характеристики данных и tidygraph для анализа графов.
Структура и характеристики геопространственных сетей выходят за рамки стандартной топологии графов, и поэтому при их анализе крайне важно явно учитывать пространственные особенности, например, географические проекции. В библиотеку sfnetworks внедрены процедуры расчета кратчайшего пути, очистки сети и модификации топологии, что в совокупности с возможностями интегрирования в рабочие процессы tidyverse, делает ее великолепным инструментом. Отметим сходство данного инструмента с известной библиотекой OSMnx языка программирования Python.
Библиотеку sfnetworks можно установить одним из способов: из репозитория CRAN
install.packages("sfnetworks")либо с GitHub
remotes::install_github("luukvdmeer/sfnetworks")Загрузим библиотеки:
library(tidyverse)
library(magrittr)
# для работы с геоданными
library(sf)
# работа с графами
library(sfnetworks)
library(tidygraph)
# annotation scale
library(ggspatial)В качестве примера мы используем граф дорожной сети города Барнаула. С помощью библиотеки osmdata загрузим из OpenStreetMap данные дорожной сети и визуализируем их также, как описано в предыдущей записи блога.
base_map +
# географические границы города
coord_sf(xlim = c(83.5, 83.91),
ylim = c(53.25, 53.40),
expand = FALSE) 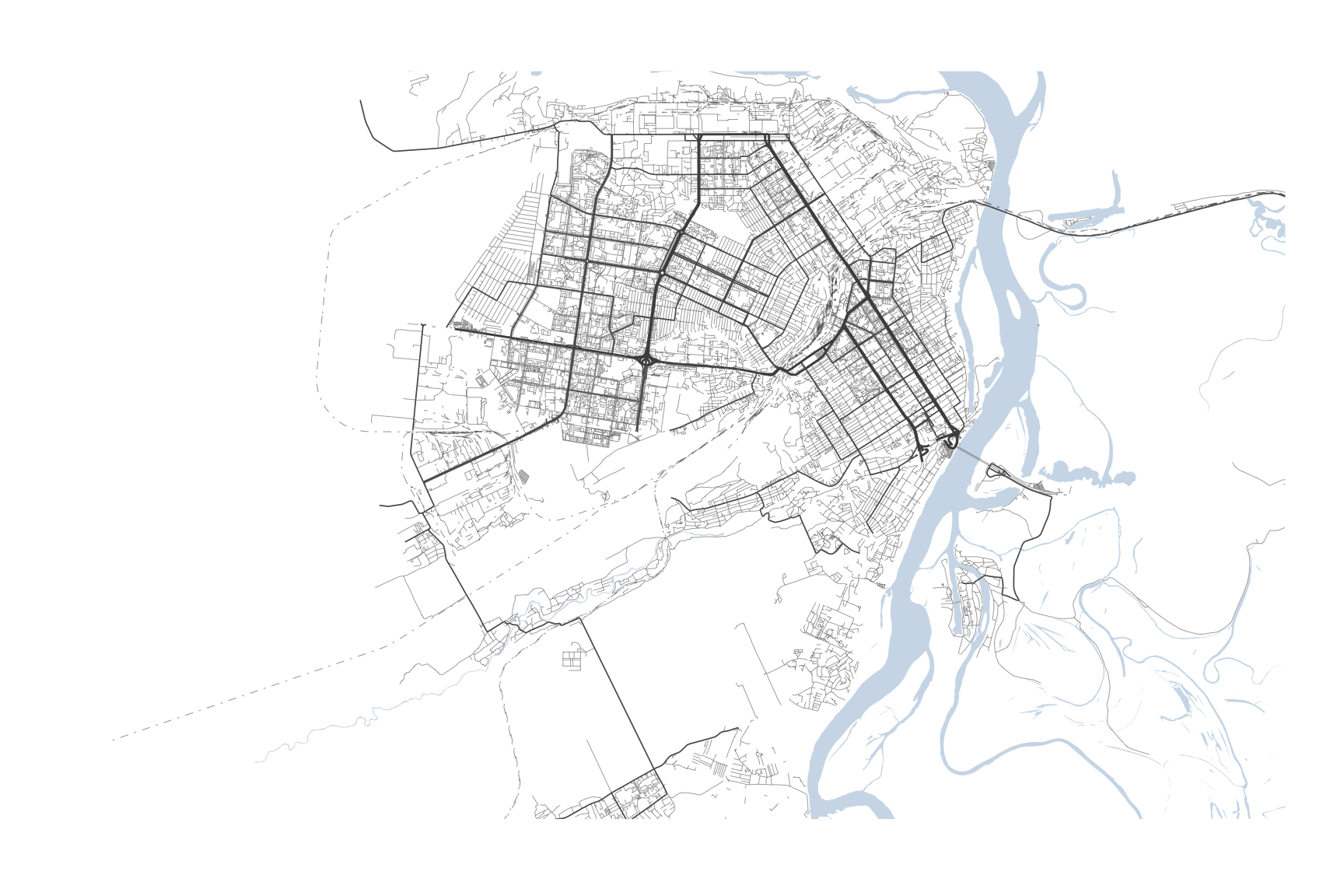
Рисунок 1: Базовая карта города Барнаула
Напомним, что базовая карта состоит из трех основных структур: streets, railways и water. В частности, streets имеет структуру:
streets## Simple feature collection with 10883 features and 10 fields
## Geometry type: LINESTRING
## Dimension: XY
## Bounding box: xmin: 83.59933 ymin: 53.1839 xmax: 83.96929 ymax: 53.52105
## CRS: EPSG:4326
## First 10 features:
## osm_id name name.en highway maxspeed oneway surface
## 1 22777674 <NA> <NA> secondary <NA> yes <NA>
## 2 24045736 Мало-Олонская улица <NA> residential <NA> <NA> <NA>
## 3 24045808 <NA> <NA> primary_link <NA> yes <NA>
## 4 24045947 Молодёжная улица <NA> tertiary <NA> <NA> <NA>
## 5 26489569 улица Димитрова <NA> residential <NA> <NA> asphalt
## 6 26489570 улица Чернышевского <NA> residential <NA> <NA> asphalt
## 7 26489571 Сибирский проспект <NA> residential <NA> <NA> asphalt
## 8 26489573 Путиловская улица <NA> residential <NA> <NA> asphalt
## 9 26489574 бульвар 9 Января <NA> living_street <NA> <NA> <NA>
## 10 26489578 улица Воровского <NA> secondary <NA> yes <NA>
## length highway_group size geometry
## 1 75.75878 medium 0.3 LINESTRING (83.78562 53.322...
## 2 124.03223 small 0.2 LINESTRING (83.79758 53.328...
## 3 557.15516 large 0.3 LINESTRING (83.79939 53.327...
## 4 479.84454 medium 0.3 LINESTRING (83.78218 53.350...
## 5 372.71826 small 0.2 LINESTRING (83.79013 53.349...
## 6 551.44589 small 0.2 LINESTRING (83.79074 53.343...
## 7 121.67048 small 0.2 LINESTRING (83.78277 53.356...
## 8 292.56884 small 0.2 LINESTRING (83.78761 53.356...
## 9 246.92119 small 0.2 LINESTRING (83.78713 53.367...
## 10 625.88168 medium 0.3 LINESTRING (83.79632 53.367...Здесь указаны: LINESTRING – последовательность точек, соединенных прямыми, непересекающимися отрезками линий; одномерная геометрия XY; значения ключа highway (основной тег, указывающий тип дорог); maxspeed – максимальная разрешенная скорость; oneway – является ли дорога с односторонним движением; surface – дорожное покрытие. Используем данную информацию для визуализации карт.
Максимальная разрешенная скорость
# добавим максимально разрешенную скорость
streets <-
streets %>%
mutate(max_speed = as.numeric(maxspeed)) %>%
dplyr::mutate(max_speed = replace_na(max_speed, 0))# максимальная разрешенная скорость из OSM на карте
base_map +
geom_sf(data = streets %>%
dplyr::filter(max_speed > 0),
aes(color = as.factor(max_speed))) +
# географические границы города
coord_sf(xlim = c(83.57, 83.88),
ylim = c(53.31, 53.40),
expand = FALSE) +
ggsci::scale_color_lancet() +
labs(color = "максимальная разрешенная скорость (км/ч):")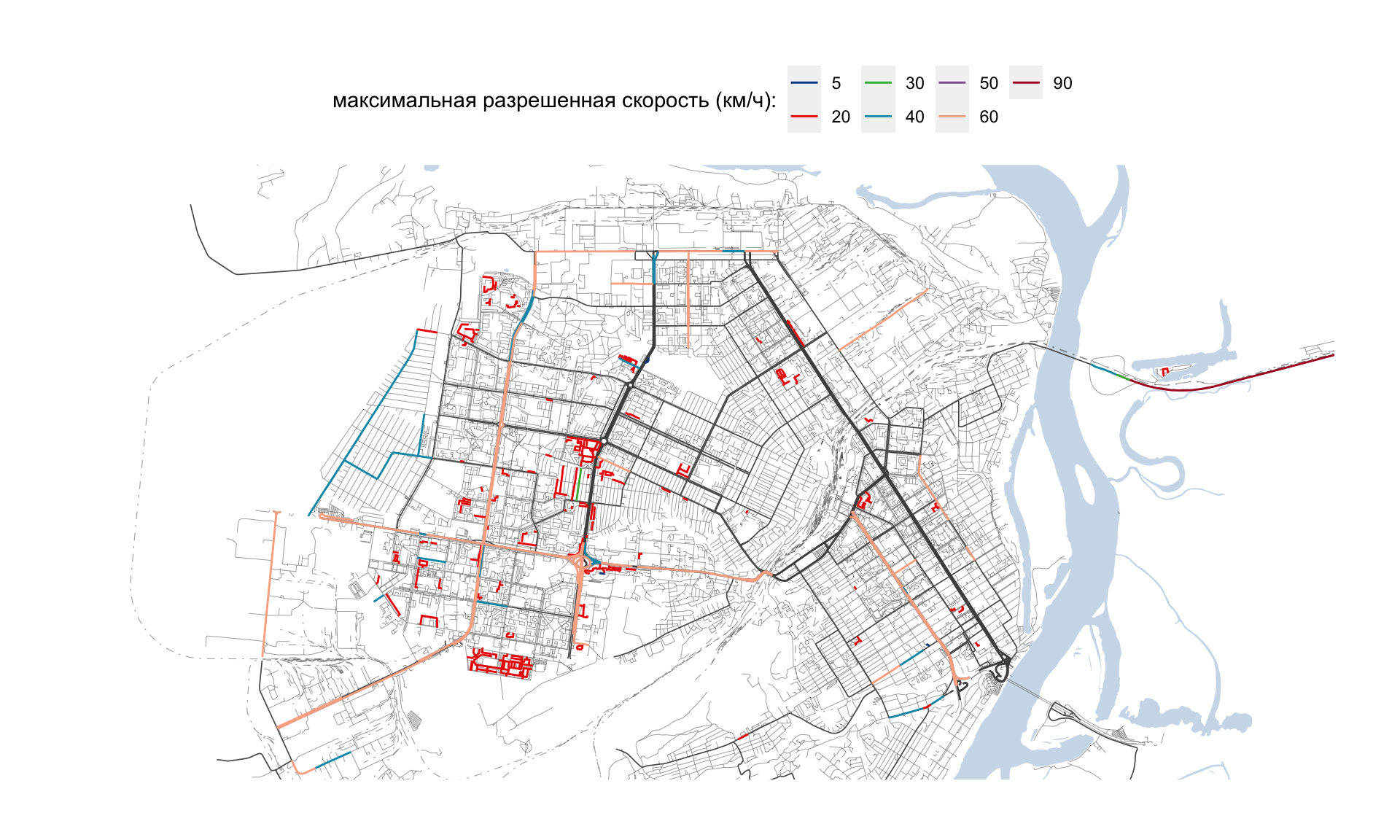
Рисунок 2: Максимальная разрешенная скорость на дорогах г. Барнаула по версии OpenStreetMap
Дорожное покрытие
# дорожное покрытие по версии OpenStreetMap
base_map +
geom_sf(data = streets,
aes(color = as.factor(surface))) +
# географические границы города
coord_sf(xlim = c(83.57, 83.88),
ylim = c(53.31, 53.40),
expand = FALSE) +
labs(color = "дорожное покрытие:") +
scale_color_viridis_d(option = "viridis", direction = 1)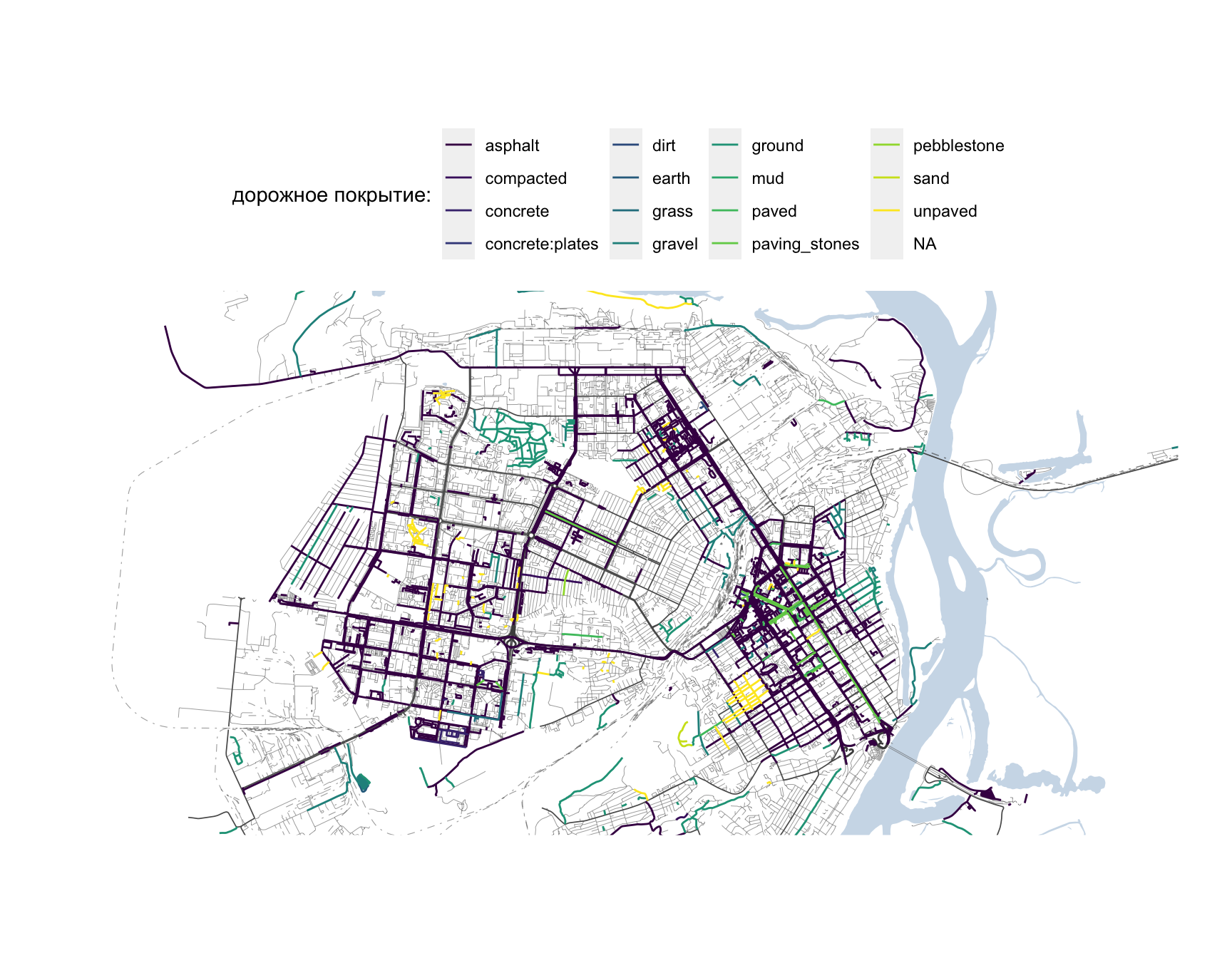
Рисунок 3: Дорожное покрытие дорог г. Барнаула по версии OpenStreetMap
Одностороннее движение
# улицы с односторонним движением
base_map +
geom_sf(data = streets %>%
dplyr::filter(oneway == "yes"),
color = "blue") +
# географические границы города
coord_sf(xlim = c(83.57, 83.88),
ylim = c(53.31, 53.40),
expand = FALSE)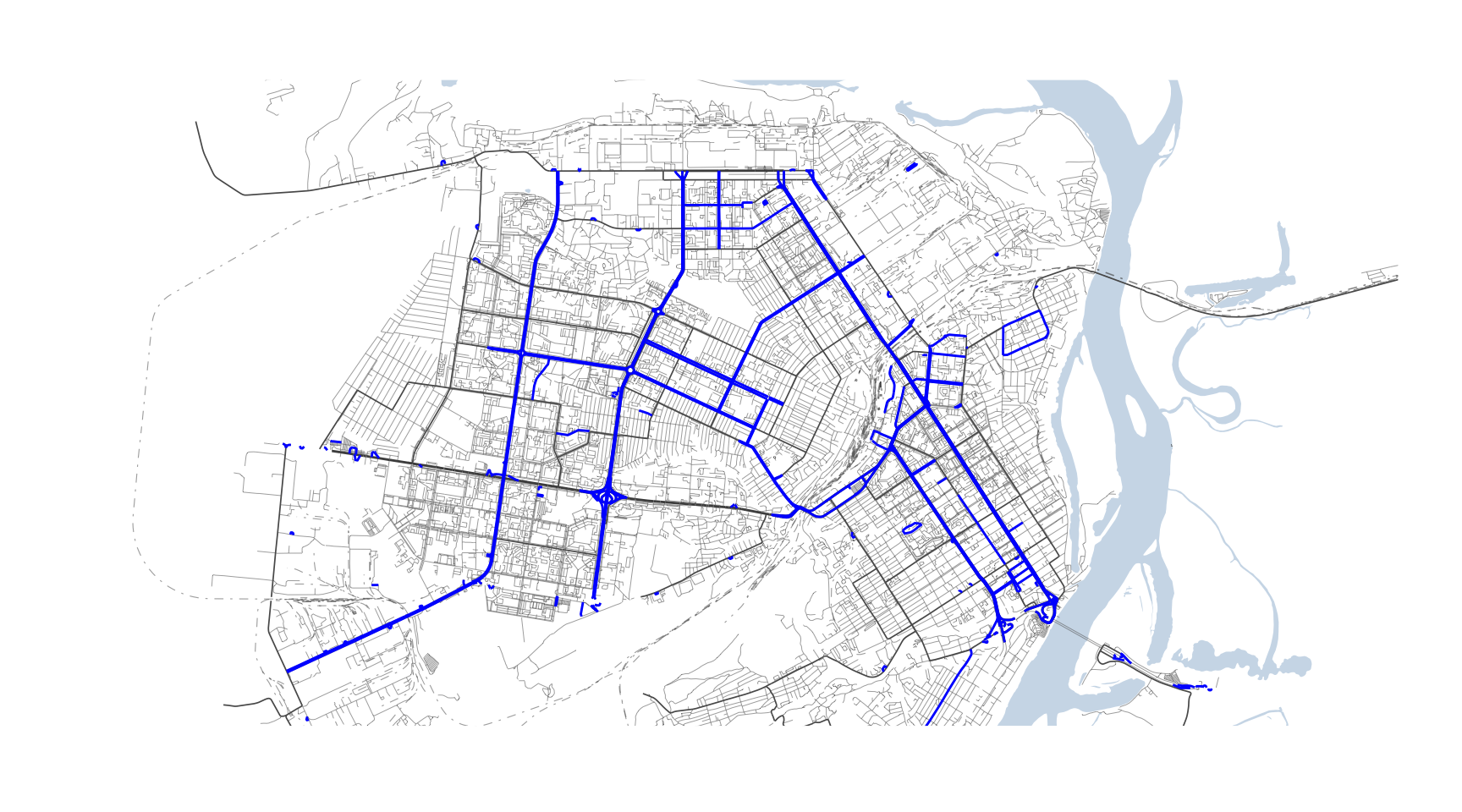
Рисунок 4: Улицы с односторонним движением г. Барнаула по версии OpenStreetMap
Как мы видим, OpenStreetMap предоставляет не так много информации, тем не менее, эту информацию можно использовать для анализа дорожной сети.
Граф дорожной сети
Чтобы сделать граф из дорожной сети нужна буквально одна команда из библиотеки sfnetworks!
net <- as_sfnetwork(streets) %>%
# географическая проекция
st_transform(4326) # граф дорожной сети Барнаула (кроп)
ggplot() +
geom_sf(data = st_as_sf(net, "edges"),
col = "black", alpha = 0.4) +
geom_sf(data = st_as_sf(net, "nodes"),
col = "black", alpha = 0.4,
size = 0.6) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.57, 83.82),
ylim = c(53.31, 53.40),
expand = FALSE) 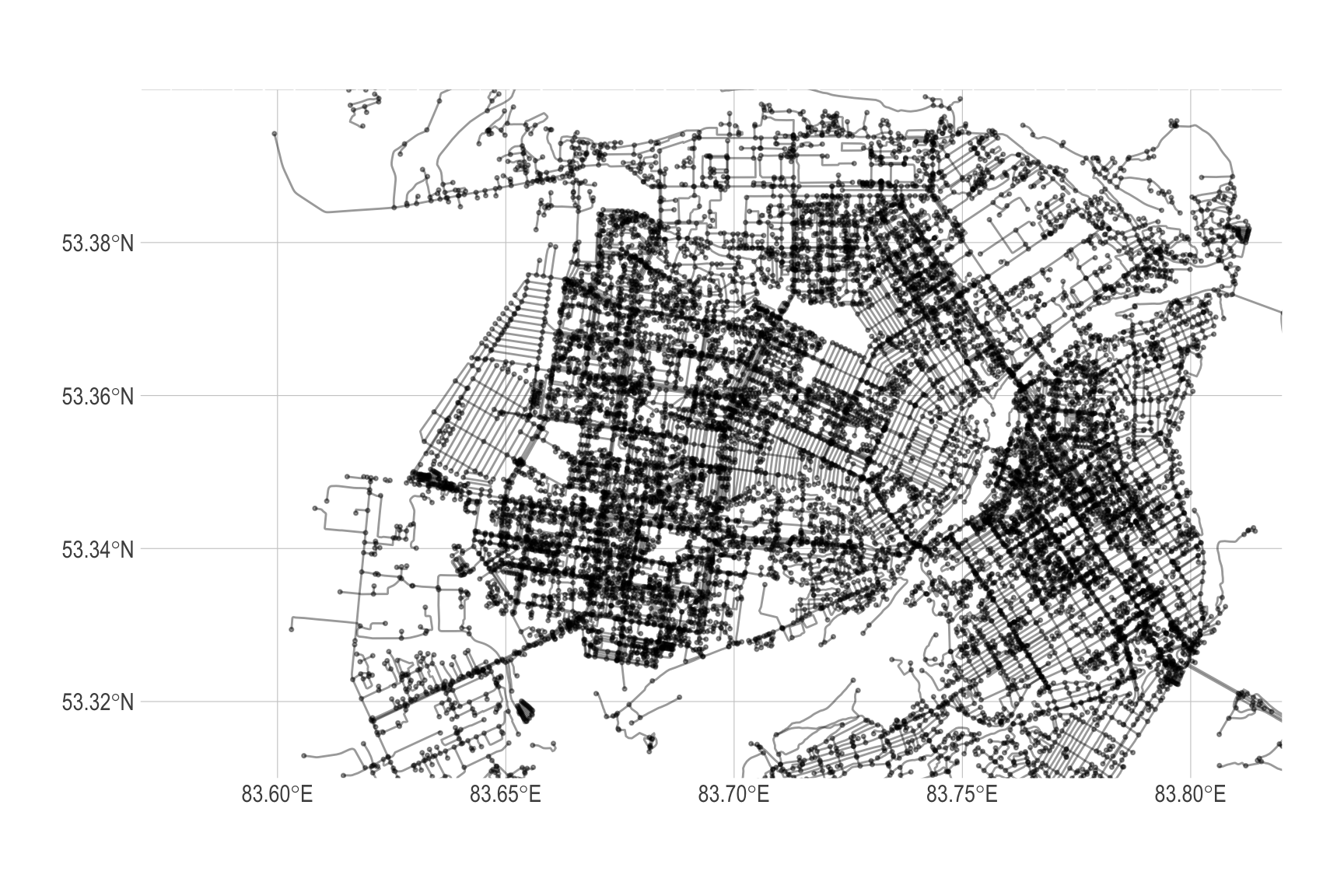
Рисунок 5: Граф дорожной сети г. Барнаула
Рассмотрим таблицу содержащую координаты вершин графа.
# вершины графа (чтобы потом можно было сделать плотности)
our_nodes <- st_as_sf(net, "nodes")$geometry %>%
st_coordinates() %>%
as_tibble() %>%
rename(lon = X,
lat = Y)Следующая карта показывает, где сосредоточено максимальное число узлов (соотвественно, городских перекрестков).
# базовая карта + граф дорожной сети Барнаула (кроп с плотностями)
ggplot() +
stat_density_2d(data = our_nodes,
aes(fill = stat(nlevel), x = lon, y = lat),
geom = "polygon",
n = 300, bins = 15, contour = TRUE, alpha = 0.2) +
geom_sf(data = st_as_sf(net, "edges"), col = "black", alpha = 0.4) +
geom_sf(data = st_as_sf(net, "nodes"), col = "black", alpha = 0.3, size = 0.2) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.57, 83.82),
ylim = c(53.31, 53.40),
expand = FALSE) +
viridis::scale_fill_viridis(discrete = F,
option = "viridis",
direction = 1) +
labs(x = "", y = "",
fill = "нормированное количество узлов графа:") +
theme(legend.position = "none")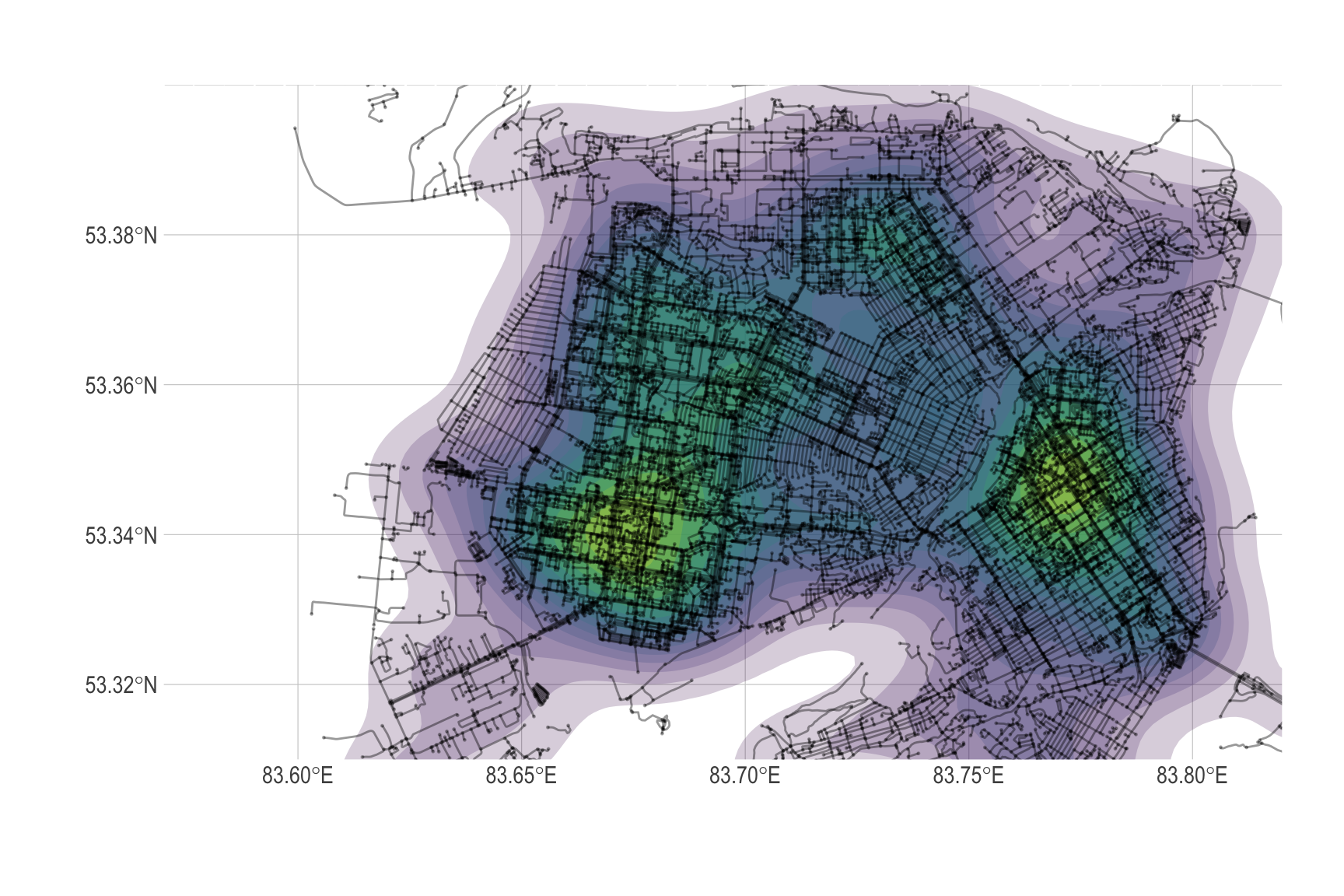
Рисунок 6: Плотность узлов графа дорожной сети г. Барнаула
Сглаживание графа дорожной сети
Некоторые узлы графа могут содержаться внутри ребра и не использоваться для вычисления кратчайшего пути. Такого рода узлы мы назовем псевдоузлами. Для уменьшения сложности графа их удаляют, проводя процедуру сглаживания.
smoothed_net <- convert(net, to_spatial_smooth)# граф дорожной сети Барнаула (сглаживание)
ggplot() +
geom_sf(data = st_as_sf(smoothed_net, "edges"),
col = "black", alpha = 0.4) +
geom_sf(data = st_as_sf(smoothed_net, "nodes"),
col = "black", alpha = 0.4,
size = 0.6) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.65, 83.74),
ylim = c(53.35, 53.39),
expand = FALSE) 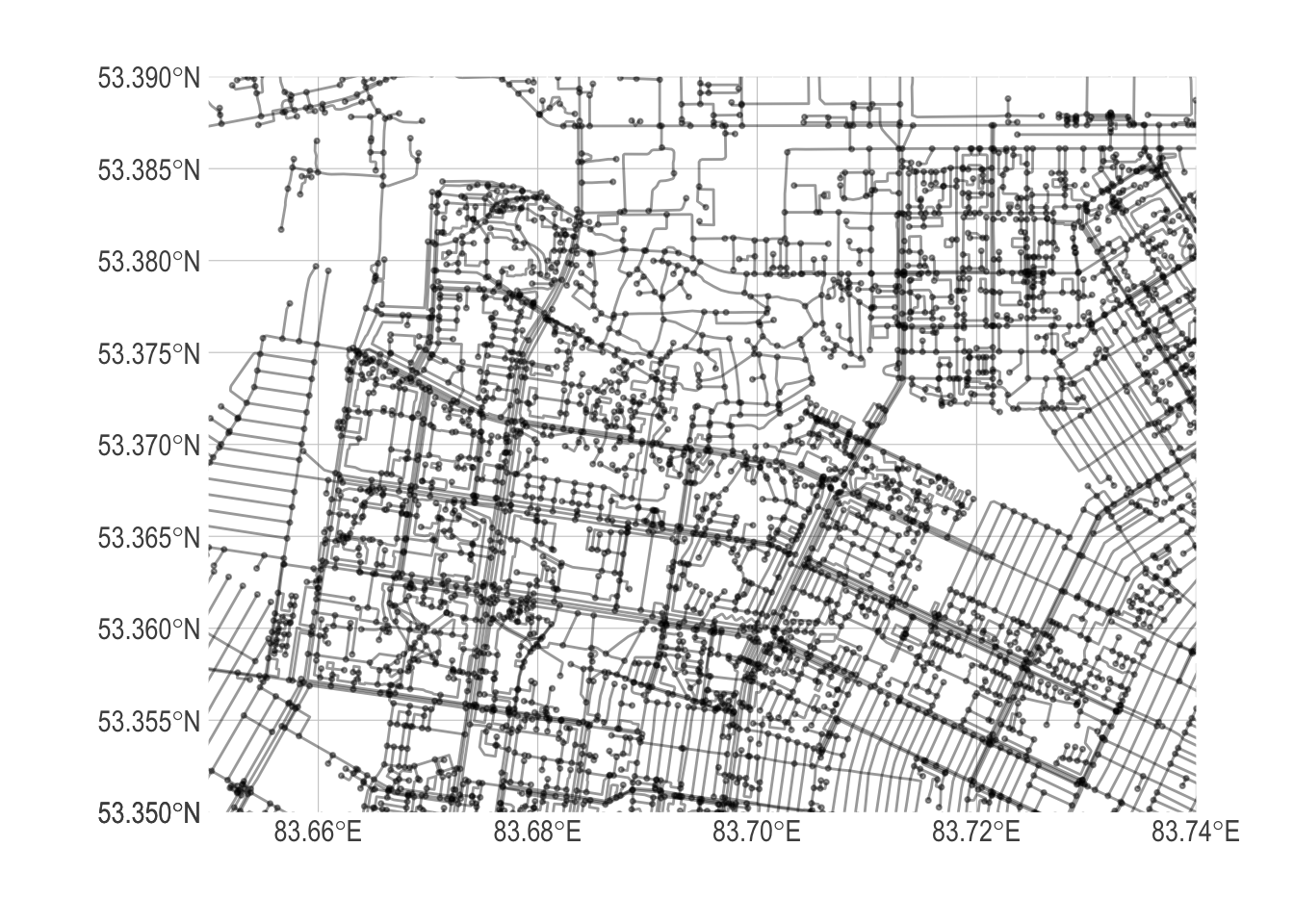
Рисунок 7: Упрощенный (сглаженный) граф дорожной сети г. Барнаула
Анализ графа дорожной сети
Основу библиотеки sfnetworks с точки зрения графов составляет библиотека tidygraph содержащая богатые возможности для анализа.
Центральность узлов графа
Рассмотрим понятие центральности узла графа. Показатель центральности или близости к центру в теории графов и анализе сетей определяет наиболее важные вершины графа.
Существует множество различных определений центральности. Например, функция centrality_betweenness() вводит понятие центральности, которое определяется количеством геодезических (кратчайших путей), проходящих через вершину (ребро), иными словами, это cтепень посредничества вершины (ребра) графа. Таким образом, мы можем выделить наиболее важные перекрестки через которые проходит наибольший транспортный поток.
net <- net %>%
activate("nodes") %>%
mutate(bc = centrality_betweenness())# кроп с центральными узлами
base_map +
geom_sf(data = st_as_sf(net, "edges"), col = "black", alpha = 0.2) +
geom_sf(data = st_as_sf(net, "nodes"),
aes(col = bc/1000, size = bc/1000, alpha = bc/1000)) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.57, 83.82),
ylim = c(53.31, 53.40),
expand = FALSE) +
viridis::scale_color_viridis(option = "inferno", direction = 1) +
labs(size = "степень посредничества вершины графа (тыс. ед.):",
alpha = "",
color = "") +
theme(legend.position = "bottom") +
guides(size = guide_legend(order = 1, ncol = 1),
alpha = guide_legend(override.aes =
list(size = 4),
order = 2, ncol = 1),
color = guide_legend(override.aes =
list(alpha = 1, size = 4),
order = 3, ncol = 1))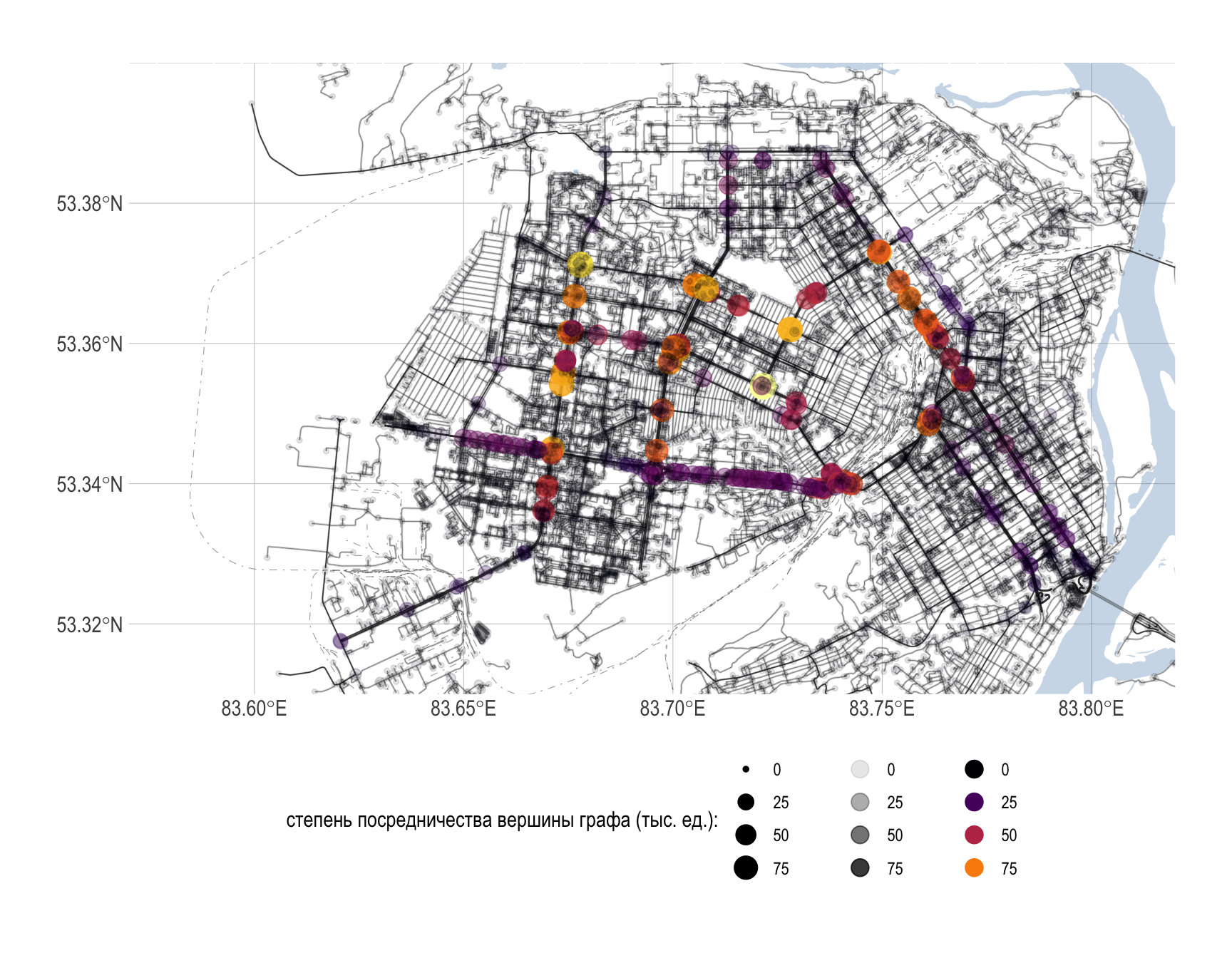
Рисунок 8: Центральность узлов графа дорожной сети г. Барнаула
net <- net %>%
activate("edges") %>%
mutate(bc_e = centrality_edge_betweenness())# кроп с центральными узлами
base_map +
geom_sf(data = st_as_sf(net, "edges"),
aes(col = bc_e/1000, size = bc_e/1000, alpha = bc_e/1000)) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.57, 83.82),
ylim = c(53.31, 53.40),
expand = FALSE) +
viridis::scale_color_viridis(option = "inferno", direction = 1) +
labs(size = "степень посредничества ребра графа (тыс. ед.):",
alpha = "",
color = "") +
theme(legend.position = "bottom") +
guides(size = guide_legend(order = 1, ncol = 1),
alpha = guide_legend(override.aes =
list(size = 4),
order = 2, ncol = 1),
color = guide_legend(override.aes =
list(alpha = 1, size = 4),
order = 3, ncol = 1))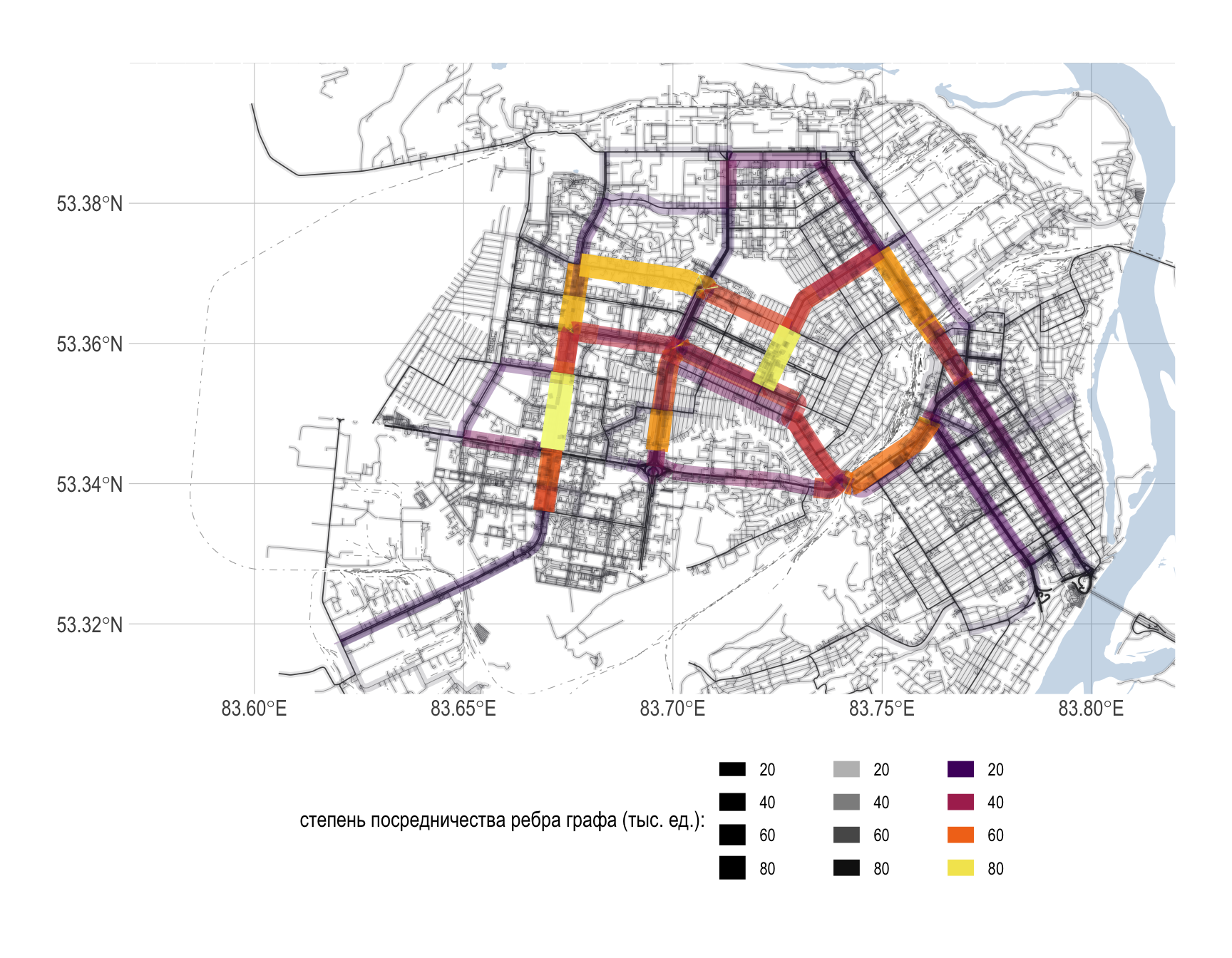
Рисунок 9: Центральность ребер графа дорожной сети г. Барнаула
Связность графа
Ключевую роль в определении связности графа играют cut edges (cut nodes) – ребра (вершины) графа, при удалении которых нарушается связность графа. С точки зрения дорожной сети, это те ключевые улицы (перекрестки), при блокировании которых автомобиль не может попасть в другую часть города.
# cut nodes & edges
new_net <- net %>%
activate("nodes") %>%
mutate(is_cut = node_is_cut()) %>%
morph(to_linegraph) %>%
mutate(is_cut = node_is_cut()) %>%
unmorph()
cut_nodes <- new_net %>%
activate("nodes") %>%
filter(is_cut) %>%
st_geometry()
cut_edges <- new_net %>%
activate("edges") %>%
filter(is_cut) %>%
st_geometry()# cut edges
base_map +
geom_sf(data = st_as_sf(net, "edges"), col = "black", alpha = 0.2) +
geom_sf(data = st_as_sf(net, "nodes"), col = "black", alpha = 0.2) +
geom_sf(data = st_as_sf(cut_edges, "nodes"), col = "red", alpha = 0.9) +
# географические границы города
coord_sf(xlim = c(83.57, 83.88),
ylim = c(53.31, 53.40),
expand = FALSE)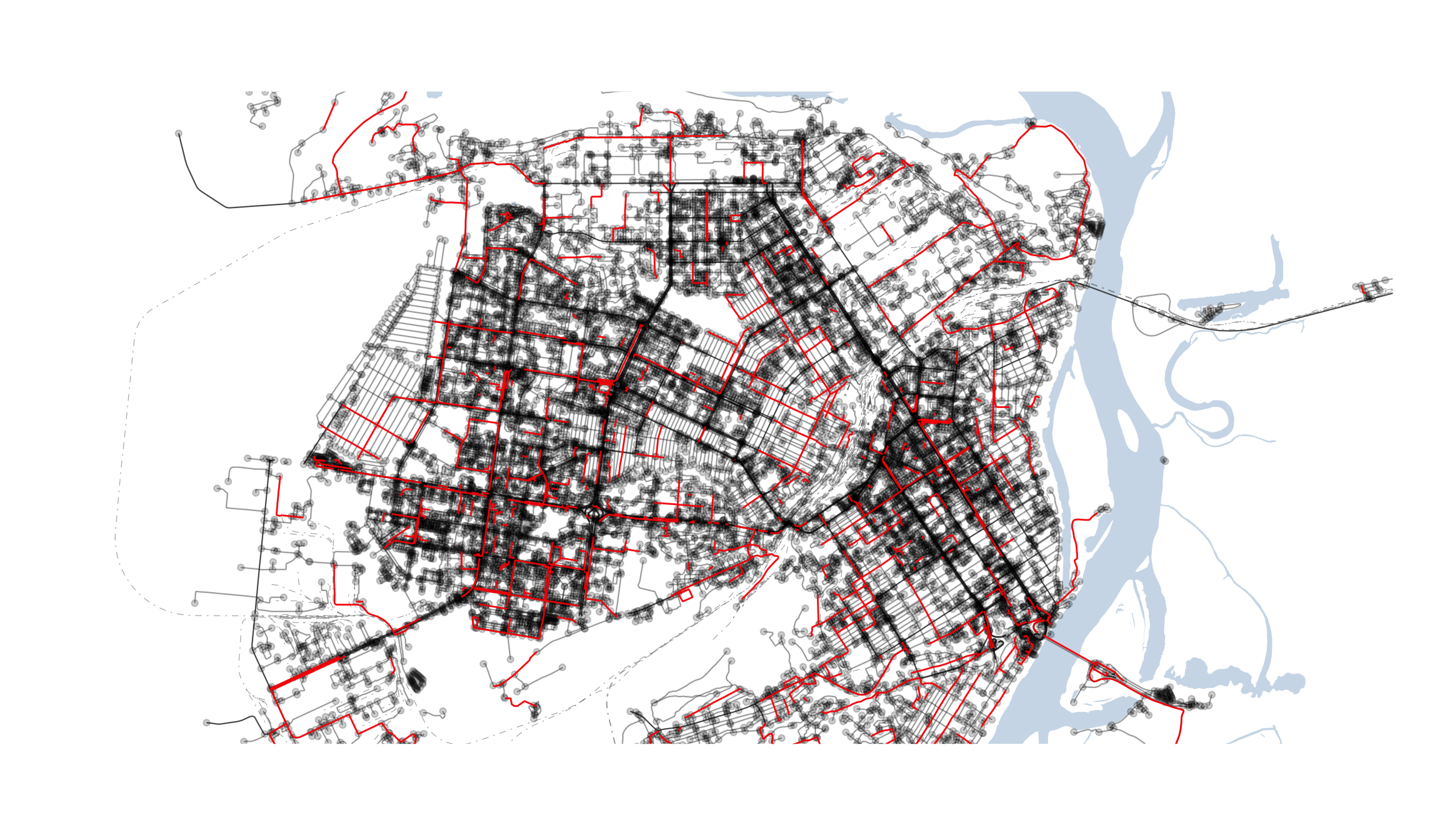
Рисунок 10: Cut edges графа дорожной сети г. Барнаула
# cut nodes
base_map +
geom_sf(data = st_as_sf(net, "edges"), col = "black", alpha = 0.2) +
geom_sf(data = st_as_sf(net, "nodes"), col = "black", alpha = 0.2) +
geom_sf(data = st_as_sf(cut_nodes, "nodes"), col = "red", alpha = 0.5) +
# географические границы города
coord_sf(xlim = c(83.57, 83.88),
ylim = c(53.31, 53.40),
expand = FALSE)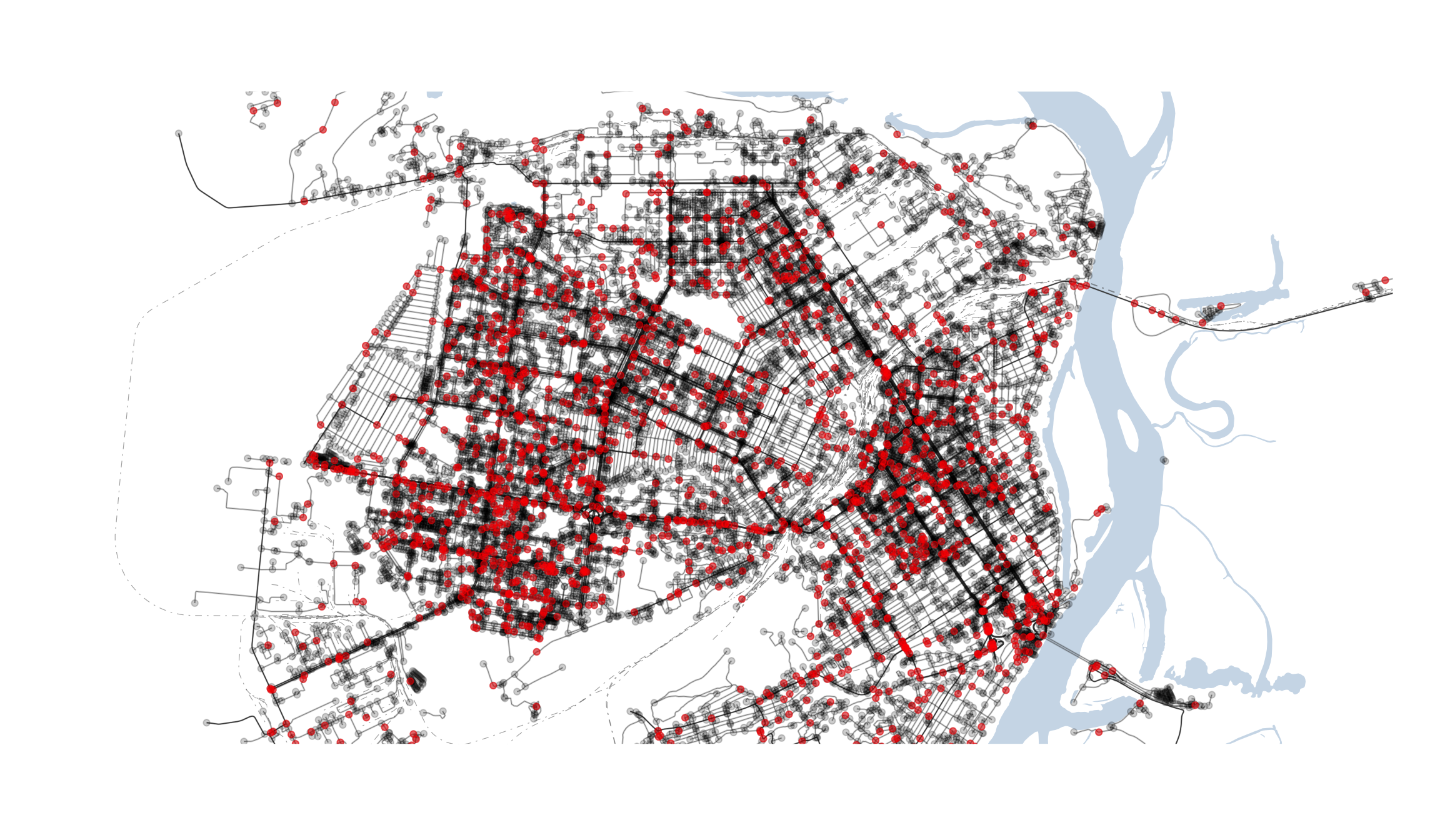
Рисунок 11: Cut nodes графа дорожной сети г. Барнаула
Нахождение кластеров
Существует множество различных алгоритмов для кластеризации узлов графа. Ниже используется метод Лувена для обнаружения кластеров (сообществ).
con_net <- as_sfnetwork(streets, directed = F) %>%
# географическая проекция
st_transform(4326) %>%
activate("nodes") %>%
filter(group_components() == 1)
custered_net <-
con_net %>%
activate("nodes") %>%
mutate(louvain = as.factor(group_louvain()))base_map +
geom_sf(data = st_as_sf(con_net, "edges"),
col = "black", alpha = 0.4) +
geom_sf(data = st_as_sf(custered_net, "nodes"),
aes(col = louvain), alpha = 0.8, size = 1.2) +
# географические границы города
coord_sf(xlim = c(83.53, 83.85),
ylim = c(53.29, 53.40),
expand = FALSE) +
theme(legend.position = "none") +
viridis::scale_color_viridis(option = "inferno", discrete = T)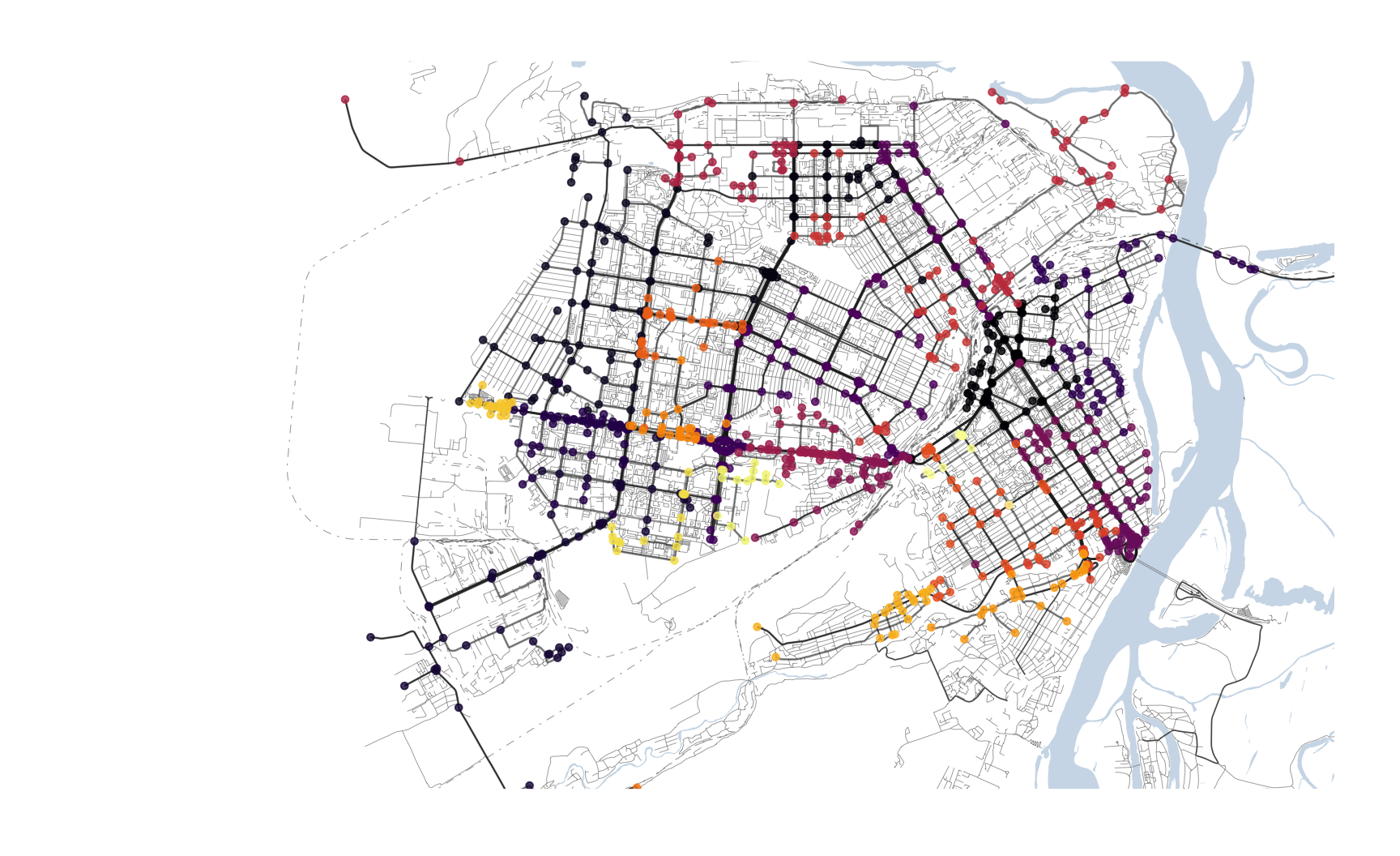
Рисунок 12: Пример кластеризации узлов графа
Азимут (направление) улиц городской структуры
Для того, чтобы проанализировать показатели застройки уличной сети дорог, можно использовать преобразования в полярной системе координат, например, вычислив азимут направления той или иной дороги.
net <-
net %>%
activate("edges") %>%
morph(to_spatial_transformed, 4326) %>%
mutate(azimuth = edge_azimuth()) %>%
unmorph()base_map +
geom_sf(data = st_as_sf(net, "edges"),
aes(col = as.numeric(azimuth)), alpha = 0.9) +
# географические границы города
coord_sf(xlim = c(83.71, 83.81),
ylim = c(53.31, 53.34),
expand = FALSE) +
scale_colour_gradientn(colours = terrain.colors(6)) +
labs(color = "азимут") +
hrbrthemes::theme_ipsum()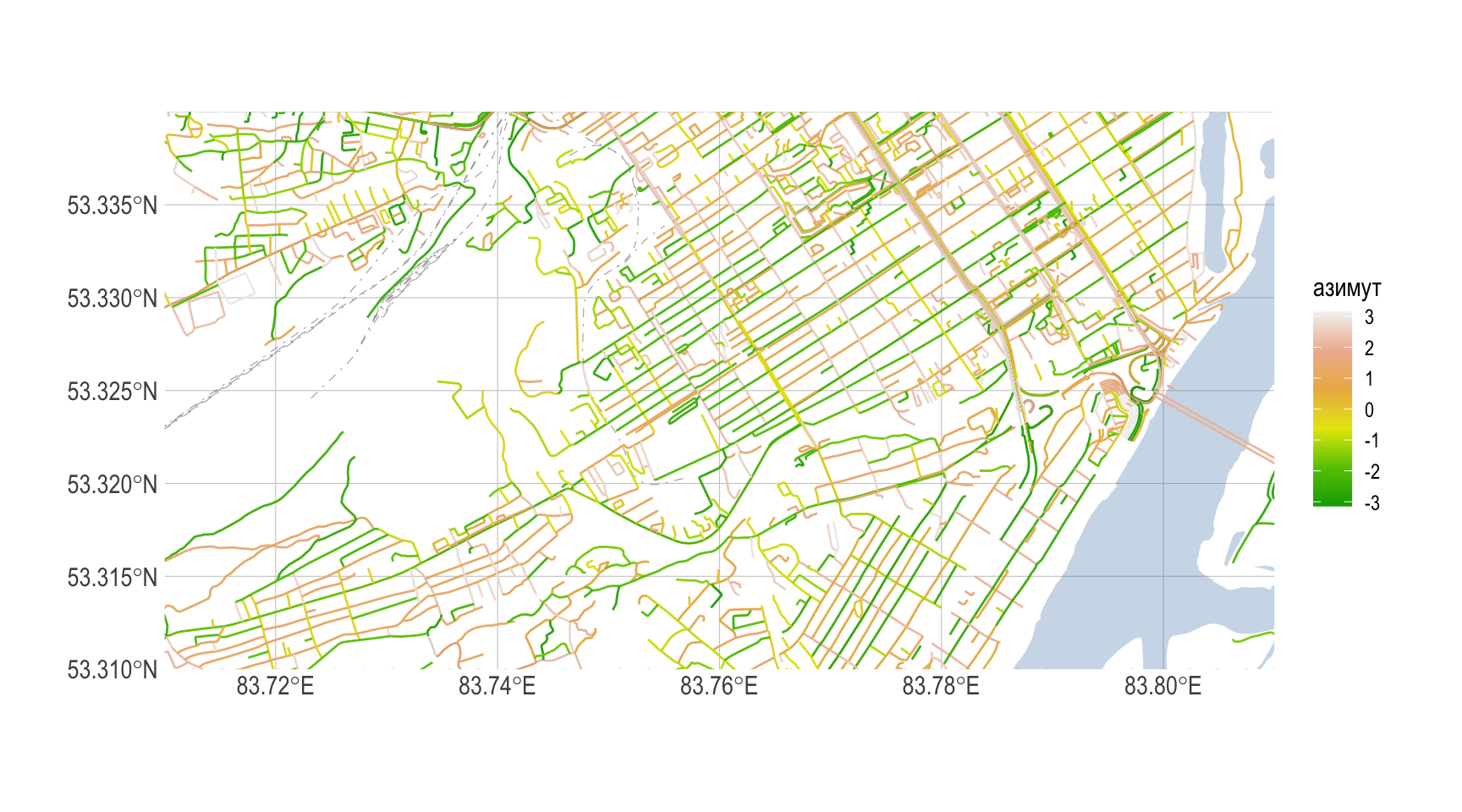
Рисунок 13: Азимуты направлений уличной сети дорог г. Барнаула
Кроме того, можно рассмотреть ориентацию дорожной сети как это сделано на странице, автором которой является Geoff Boeing.
library(units)
net %>%
pull(azimuth) %>%
as_tibble() %>%
mutate(value = round(value, 1)) %>%
group_by(value) %>%
summarise(count = n()) %>%
ggplot(aes(x = as.numeric(value), y = count)) +
geom_bar(fill = "midnightblue",
stat = "identity") +
hrbrthemes::theme_ipsum() +
labs(x = "", y = "") +
coord_polar()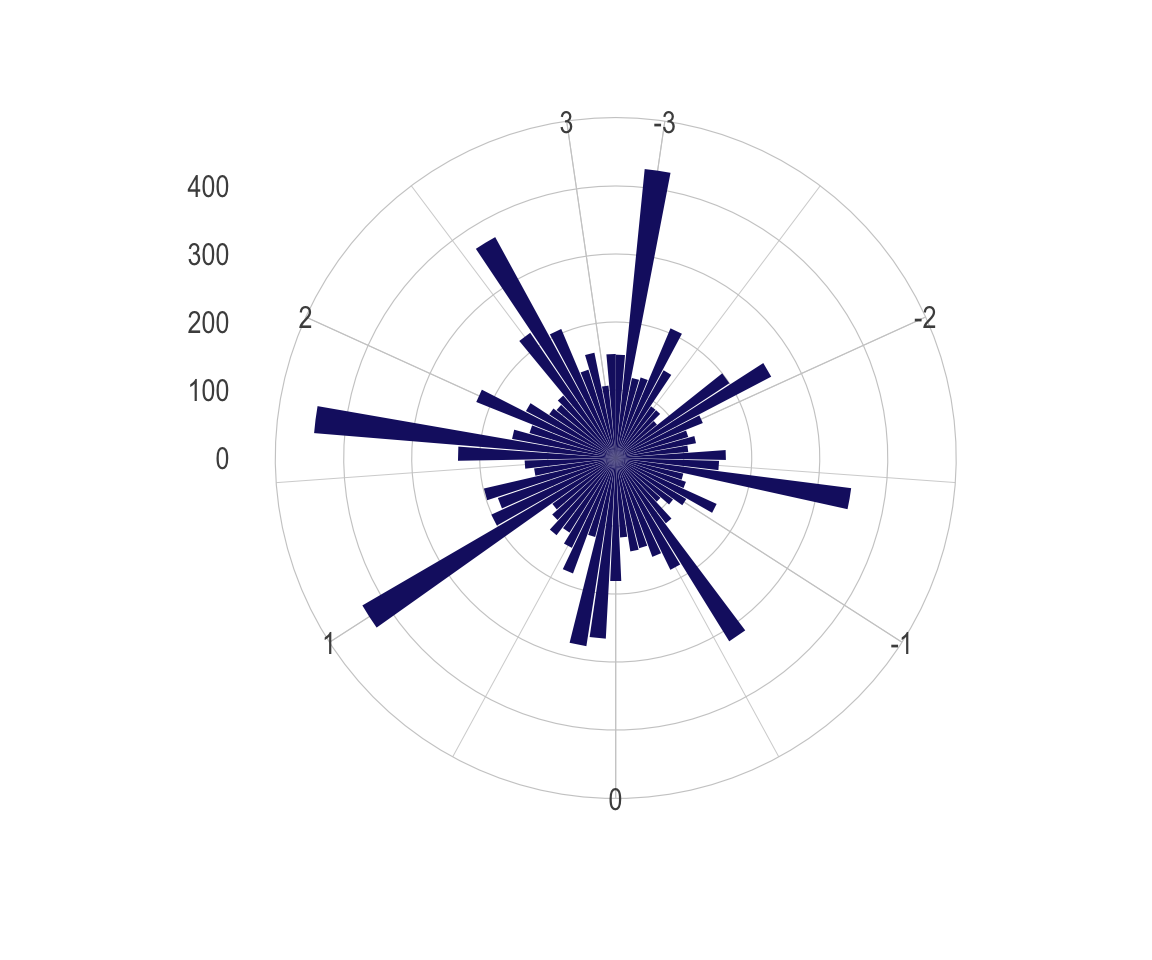
Рисунок 14: Ориентация направлений уличной сети дорог г. Барнаула
Построение областей достижимости
Одна из основных трудностей при рассмотрении достижимости узлов графа дорожной сети города, – большое количество связных компонент графа. Например, для рассматреваемой здесь дорожной сети Барнаула.
net %>% with_graph(., graph_component_count())## [1] 7267Рассмотрим одну (первую) связную компоненту графа и будем далее работать с ней.
connected_net <- net %>%
activate("nodes") %>%
filter(group_components() == 1)
connected_net %>% with_graph(., graph_component_count())## [1] 1Рассмотрим граф как объект в соответствующей географической проекции, это позволит рассмотреть вес ребра как его длину (которая будет пересчитана в метрах).
connected_net <- connected_net %>%
st_transform(4326) %>%
activate("edges") %>%
mutate(weight = edge_length())
connected_net## # A sfnetwork with 1100 nodes and 1275 edges
## #
## # CRS: EPSG:4326
## #
## # A directed multigraph with 1 component with spatially explicit edges
## #
## # Edge Data: 1,275 × 17 (active)
## # Geometry type: LINESTRING
## # Dimension: XY
## # Bounding box: xmin: 83.59933 ymin: 53.21897 xmax: 83.94187 ymax: 53.39591
## from to osm_id name name.en highway maxspeed oneway surface length
## <int> <int> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <dbl>
## 1 1 2 22777… <NA> <NA> second… <NA> yes <NA> 75.8
## 2 3 4 24045… Мало… <NA> reside… <NA> <NA> <NA> 124.
## 3 5 6 24045… <NA> <NA> primar… <NA> yes <NA> 557.
## 4 7 8 24045… Моло… <NA> tertia… <NA> <NA> <NA> 480.
## 5 9 10 26489… улиц… <NA> reside… <NA> <NA> asphalt 373.
## 6 11 12 26489… Сиби… <NA> reside… <NA> <NA> asphalt 122.
## # … with 1,269 more rows, and 7 more variables: highway_group <chr>,
## # size <dbl>, geometry <LINESTRING [°]>, max_speed <dbl>, bc_e <dbl>,
## # azimuth [rad], weight [m]
## #
## # Node Data: 1,100 × 2
## # Geometry type: POINT
## # Dimension: XY
## # Bounding box: xmin: 83.59933 ymin: 53.21897 xmax: 83.94187 ymax: 53.39591
## geometry bc
## <POINT [°]> <dbl>
## 1 (83.78562 53.32271) 25
## 2 (83.78663 53.32303) 0
## 3 (83.79758 53.32863) 18020.
## # … with 1,097 more rowsВыделим различные типы ребер.
types <- connected_net %>%
activate("edges") %>%
pull(highway) %>%
unique()
types## [1] "secondary" "residential" "primary_link" "tertiary"
## [5] "living_street" "primary" "unclassified" "service"
## [9] "tertiary_link" "footway" "secondary_link"Зададим скорости движения по различным типам дорог, здесь коэффициент пересчета позволяет перевести скорости в м/с. Также, найдем соответствующее время движения по данным дорогам в секундах.
connected_net <-
connected_net %>%
activate("edges") %>%
group_by(highway) %>%
mutate(
speed = case_when(
highway == "secondary" ~ 60 / 3.6,
highway == "residential" ~ 40 / 3.6,
highway == "primary_link" ~ 60 / 3.6,
highway == "tertiary" ~ 60 / 3.6,
highway == "living_street" ~ 40 / 3.6,
highway == "primary" ~ 60 / 3.6,
highway == "unclassified" ~ 40 / 3.6,
highway == "service" ~ 40 / 3.6,
highway == "tertiary_link" ~ 60 / 3.6,
highway == "footway" ~ 40 / 3.6,
highway == "secondary_link" ~ 60 / 3.6
)
) %>%
mutate(speed = units::set_units(speed, "m/s")) %>%
mutate(time = weight / speed) %>%
ungroup()
connected_net <- activate(connected_net, "nodes")Найдем центроид рассматриваемого графа.
p <- connected_net %>%
activate("nodes") %>%
st_geometry() %>%
st_combine() %>%
st_centroid() %>%
st_transform(4326) Теперь вычислим область графа, ограничивающую 10-минутную (600 секунд) изохрону.
iso <- connected_net %>%
filter(node_distance_from(st_nearest_feature(p, connected_net),
weights = time) <= 60 * 10)Найдем выпуклую оболочку полученной области.
iso_poly <- iso %>%
st_geometry() %>%
st_combine() %>%
st_convex_hull()
iso_poly## Geometry set for 1 feature
## Geometry type: POLYGON
## Dimension: XY
## Bounding box: xmin: 83.65805 ymin: 53.31707 xmax: 83.80255 ymax: 53.38738
## CRS: EPSG:4326## POLYGON ((83.76121 53.31707, 83.69185 53.32773,...Изобразим область 10-минутной изохроны полученной из центроида графа.
base_map +
geom_sf(data = st_as_sf(iso_poly, "edges"),
col = "orange", alpha = 0.6) +
geom_sf(data = st_as_sf(iso, "edges"),
col = "red",
alpha = 0.7) +
geom_sf(data = p,
color = "blue",
alpha = 1,
shape = 8,
size = 2.5,
stroke = 1) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.65, 83.81),
ylim = c(53.315, 53.41),
expand = FALSE) +
viridis::scale_colour_viridis(direction = 1,
option = "cividis") +
annotation_scale(location = "tl", width_hint = 0.5, style = "ticks")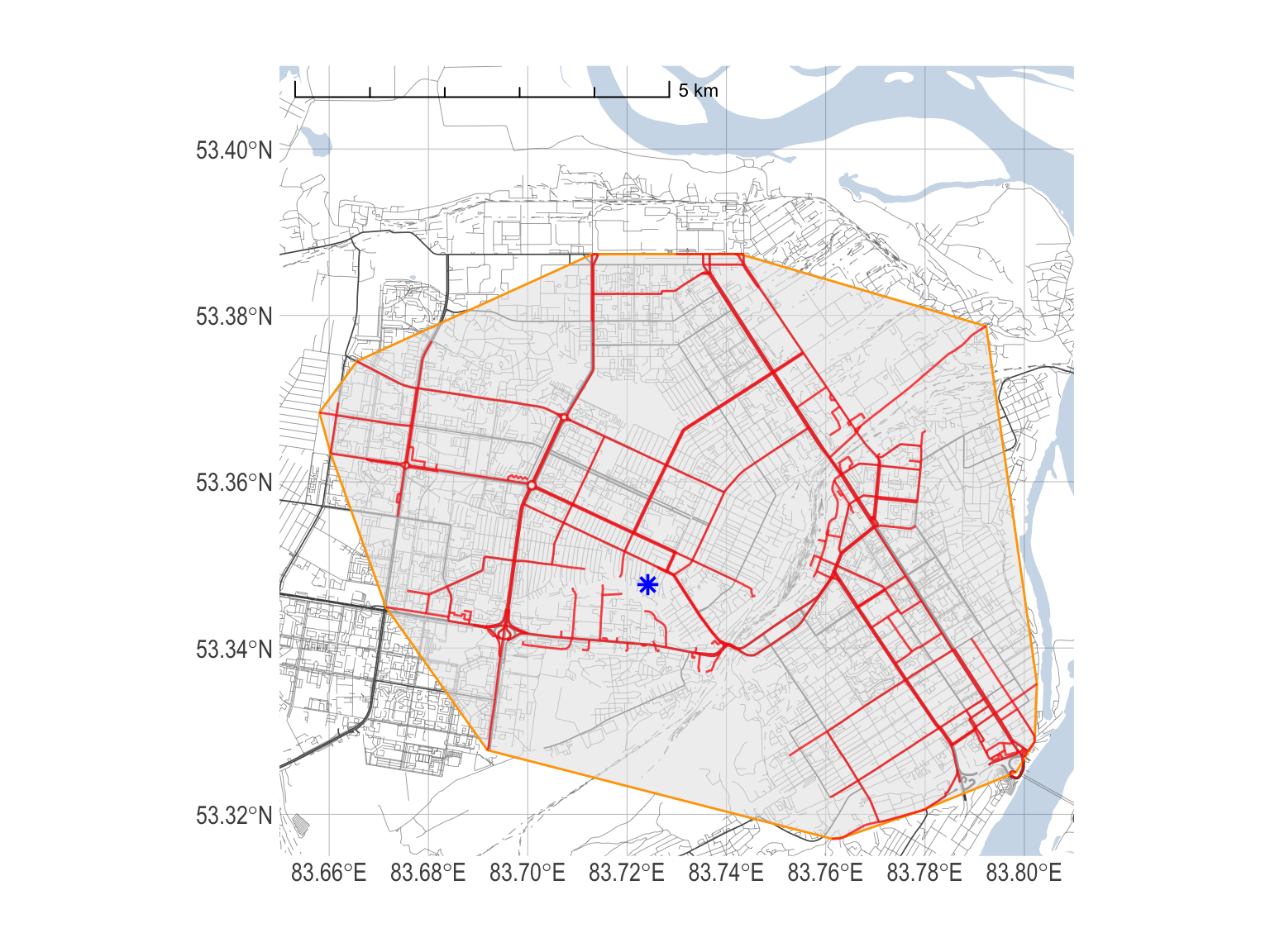
Рисунок 15: Пример построения 10-минутной изохроны
Покажем еще один способ для отображения изохрон. Для этого сформируем набор цветовой палитры на основе пороговых значений.
thresholds <- rev(seq(100, 10000, 100))
palette <- sf.colors(n = 100)Найдем множество, объединяющее все ребра и вершины графа достижимые в связной компоненте из центроида графа.
datalist_nodes = list()
for (i in c(1:100)) {
iso_data <-
convert(connected_net, to_spatial_neighborhood, p, thresholds[i]) %>%
activate("nodes") %>%
mutate(space_color = palette[i]) %>%
as_tibble()
iso_data$i <- i
datalist_nodes[[i]] <- iso_data
}
big_data_nodes <- dplyr::bind_rows(datalist_nodes)datalist_edges = list()
for (i in c(1:100)) {
iso_data <-
convert(connected_net, to_spatial_neighborhood, p, thresholds[i]) %>%
activate("edges") %>%
mutate(space_color = palette[i]) %>%
as_tibble()
iso_data$i <- i
datalist_edges[[i]] <- iso_data
}
big_data_edges <- dplyr::bind_rows(datalist_edges)Изобразим полученный результат.
base_map +
geom_sf(data = big_data_nodes, aes(color = space_color),
alpha = 0.8) +
geom_sf(data = big_data_edges, aes(color = space_color),
alpha = 0.8) +
geom_sf(data = p,
color = "black",
alpha = 1,
shape = 8,
size = 2.5,
stroke = 1) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.65, 83.81),
ylim = c(53.32, 53.41),
expand = FALSE) +
viridis::scale_colour_viridis(direction = 1,
discrete = T,
option = "plasma") +
theme(legend.position = "none") +
annotation_scale(location = "tl",
width_hint = 0.5,
style = "ticks")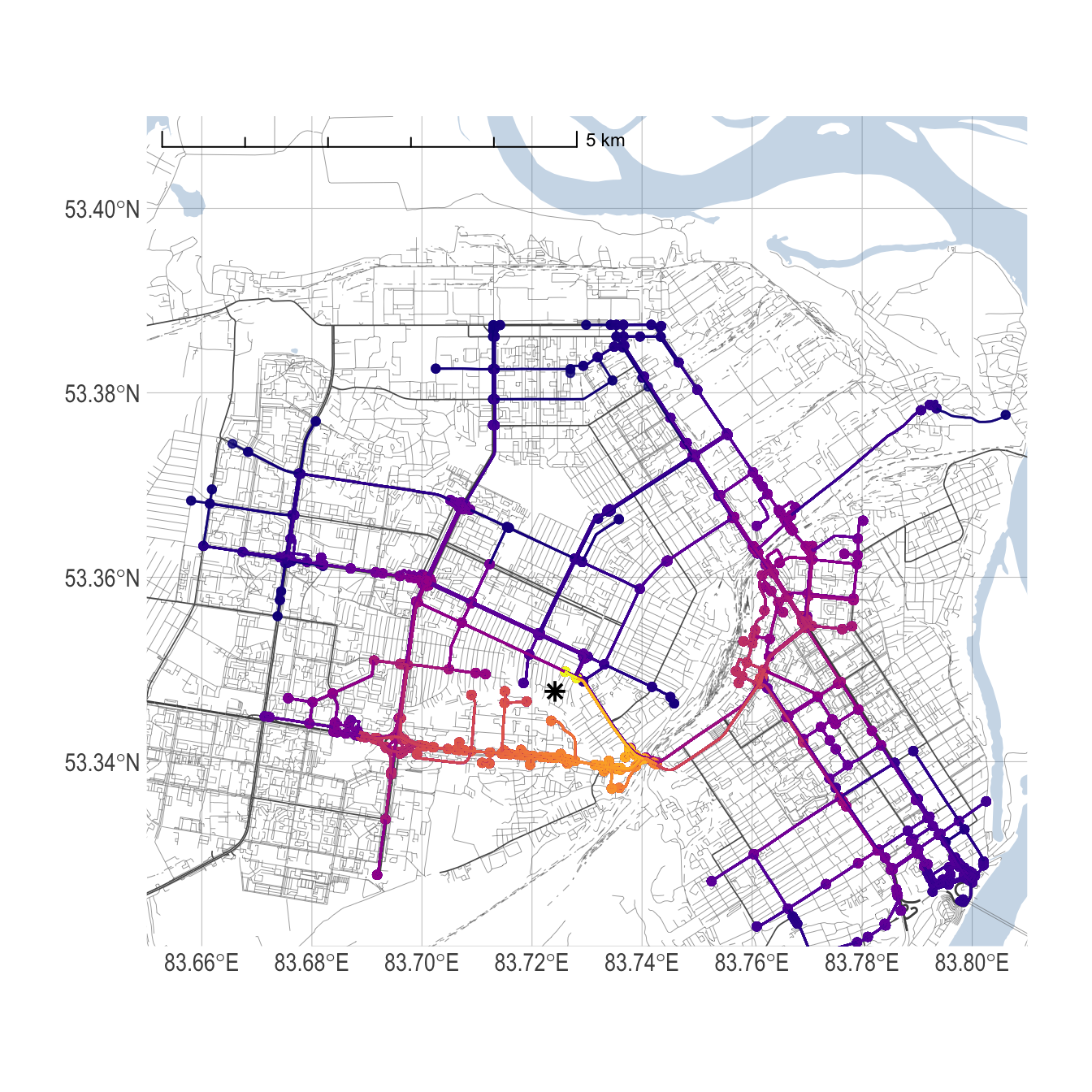
Рисунок 16: Пример построения изохроны из центроида графа
Морфемы позволяют расширить возможности работы с графами, используя dplyr с помощью команды tidygraph::morph() и затем внести полученные изменения обратно в граф командой tidygraph::unmorph(). Это позволяет вам временно изменить топологию исходной сети.
Нахождение кратчайшего пути
В sfnetworks возможно находить кратчайший путь для двух и более вершин с помощью команды-морфемы to_spatial_shortest_paths().
subnet = connected_net %>%
activate("edges") %>%
morph(
to_spatial_shortest_paths,
from = 10, to = 60,
weights = edge_length()
) %>%
mutate(in_paths = TRUE) %>%
unmorph()
p1 <- connected_net %>%
activate("nodes") %>%
st_as_sf() %>%
slice(c(10))
p2 <- connected_net %>%
activate("nodes") %>%
st_as_sf() %>%
slice(c(60))
colors = sf.colors(2, categorical = TRUE)base_map +
geom_sf(data = st_as_sf(subnet %>% filter(in_paths), "edges"),
col = "blue", alpha = 0.9, size = 1) +
geom_sf(data = p1,
color = colors[1],
alpha = 1,
shape = 8,
size = 2.5,
stroke = 1) +
geom_sf(data = p2,
color = colors[2],
alpha = 1,
shape = 8,
size = 2.5,
stroke = 1) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.65, 83.85),
ylim = c(53.29, 53.40),
expand = FALSE) 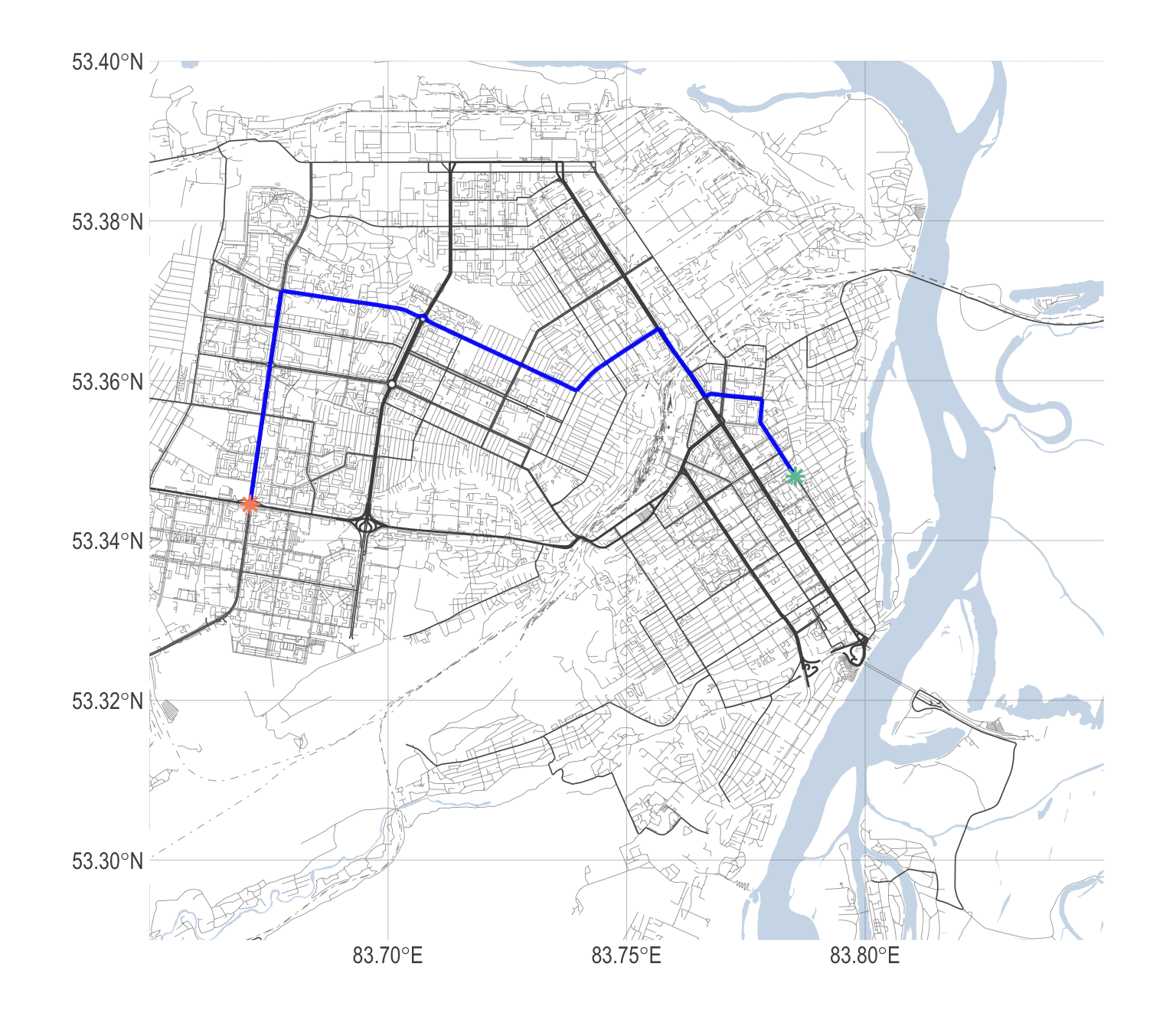
Рисунок 17: Пример построения кратчайшего пути между заданными вершинами в связной компоненте графа
Пример использования морфем показан ниже, где ищутся кратчайшие пути в связной компоненте графа из точки с исходным номером в заданный набор точек командой to_spatial_shortest_paths().
new_net <- connected_net %>%
activate("edges") %>%
morph(
to_spatial_shortest_paths,
from = 50, to = seq(from = 100, to = 500, by = 10),
weights = edge_length()
) %>%
mutate(in_paths = TRUE) %>%
unmorph()
p_from <- connected_net %>%
activate("nodes") %>%
st_as_sf() %>%
slice(c(50))Полученные пути объединим и изобразим красным цветом.
base_map +
geom_sf(data = st_as_sf(new_net, "edges"),
col = "blue", alpha = 0.4) +
geom_sf(data = st_as_sf(new_net %>% filter(in_paths), "edges"),
col = "red", alpha = 0.9, size = 1) +
geom_sf(data = p_from,
color = "black",
alpha = 1,
shape = 8,
size = 2.5,
stroke = 1) +
hrbrthemes::theme_ipsum() +
# географические границы города
coord_sf(xlim = c(83.53, 83.85),
ylim = c(53.29, 53.40),
expand = FALSE) 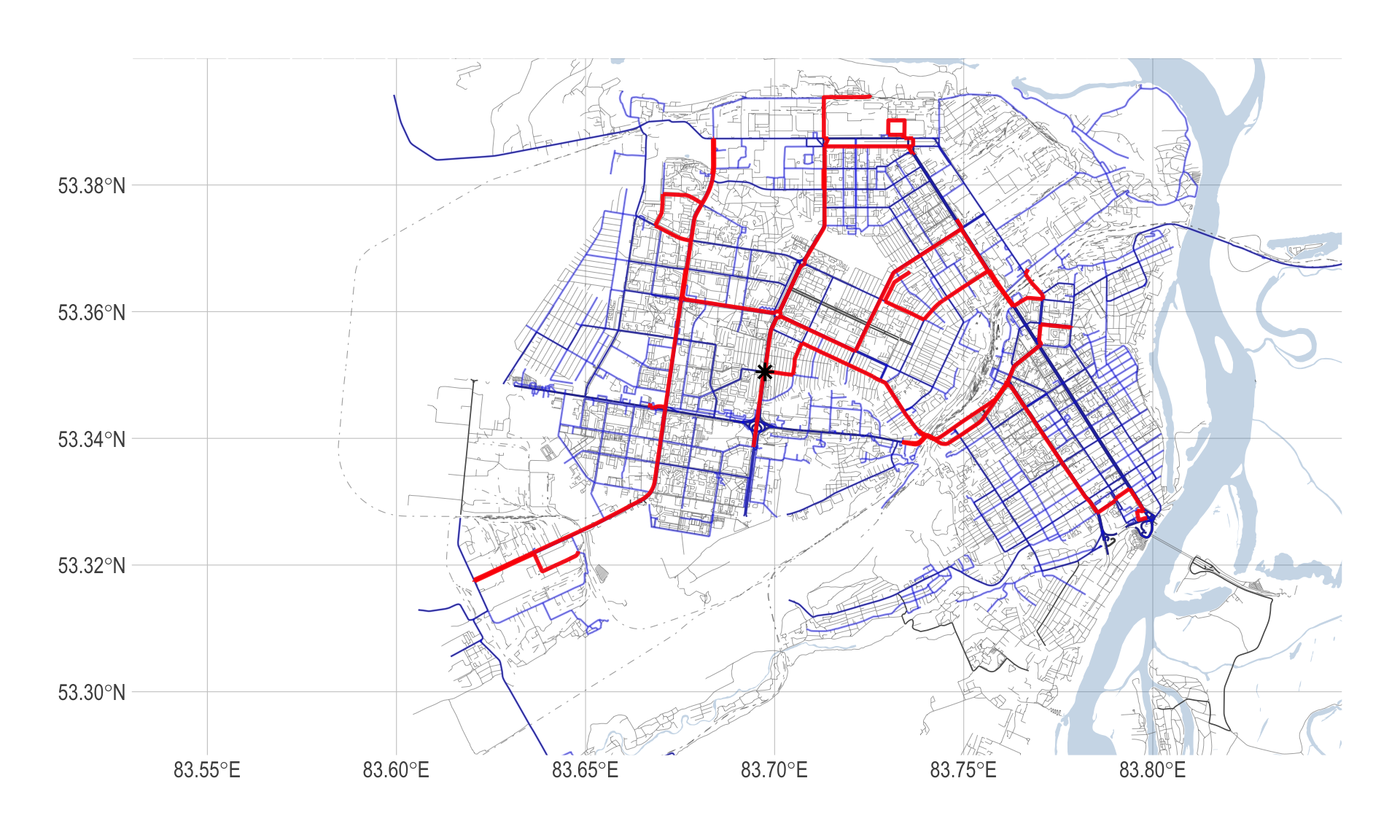
Рисунок 18: Пример построения объединения кратчайших путей между заданными вершинами в связной компоненте графа
Заключение
В статье были рассмотрены некоторые вопросы связанные с анализом структуры городской дорожной сети. Загрузив данные из OpenStreetMap и затем преобразовав их в граф дорожной сети, используя библиотеку sfnetworks, возможно работать с графом дорожной сети как математическим объектом.
Здесь были рассмотрены некоторые вопросы связанные с
- отображением информации предоставленной OpenStreetMap на карте дорожной сети;
- анализом графа дорожной сети (нахождение центральных ребер и узлов, cut edges и cut nodes, кластеров для вершин графа, ориентации направления улиц, и т.д.);
- анализом нахождения кратчайших путей и изохрон с учетом скоростей движения автомобиля.
Одной из основных технических трудностей является обилие связных компонент графа дорожной сети, что затрудняет поиск оптимальных маршрутов в силу невозможности достичь ту или иную вершину из заданной.
Гораздо более глубокий анализ данных структур предоставляют команды библиотек sfnetworks и tidygraph.